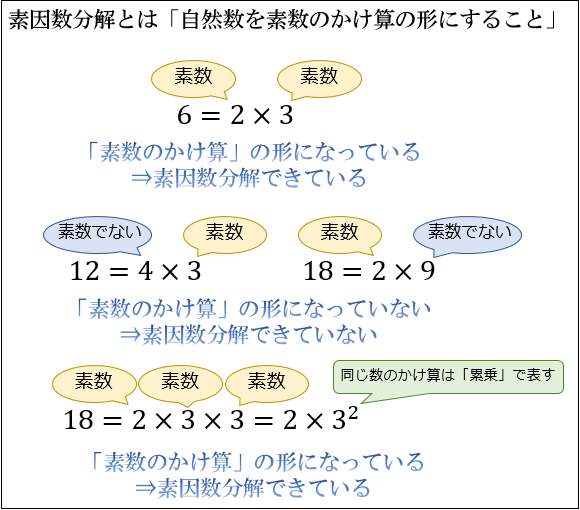
素因数分解の問題です 素因数分解の問題です nは2ケタの自然数で n/ を既約分数にしたとき 分母が5になるという このようなnは全部で何個あるか?? 答えは18となっています やり方を教えてください中学3年生 数学 因数分解 問題プリント 無料ダウンロード・印刷 、共通因数などの概念について理解し、因数分解のやり方を確認するとともに、素数、素因数分解の意味を理解し、解を求める練習ができる問題プリントです。 因数分解 (1) 答え素因数分解は「素数の積」で表わさなければならないので,次のようにただ単に「積」にしただけでは素因数分解とはいえない. ×間違いの例 12=4 × 3 (← 4 は素数でない.) ×間違いの例 30=3 × 10 (← 10 は素数でない.) 12 の素因数分解について,次の

世界一わかりやすい数学問題集中3 1章 式の展開と因数分解
素因数分解 問題答え付き
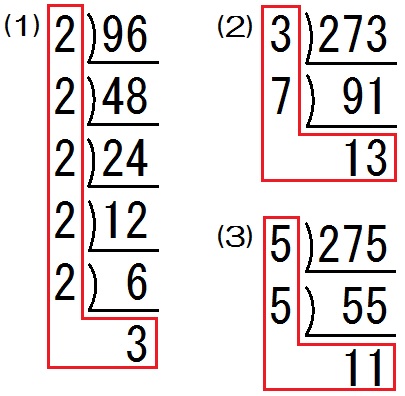
素因数分解 問題答え付き- 式の展開、乗法公式、素因数分解 単元 素因数分解, キーワード 式の展開,乗法公式,因数分解 教科書の問の問題である平方根の問題が教科書の解説を見てもあまり分からなく、私の理解力不足なんですけど、どなたか分かる方問6・問7・問8・問9を是非と2数の最大公約数と最小公倍数の求め方 例)1と144 ① それぞれ素因数分解する。 ② 素因数分解の結果を利用して,最大公約数と最小公倍数を求める。 2)1 2) 60 2) 30 3) 15 5 2)144 2) 72 2) 36 2) 18 3) 9 3 1=2*2*2 *3 *5 144=2*2*2*2*3*3



素因数分解とは やり方やコツ 利用問題 約数など 受験辞典
素因数分解は、最大公約数や最小公倍数を考えるときに便利です。 例えば↑で使った「30」と「42」で考えてみましょう。 42の素因数分解は↓ 30=2×3×5数学・算数 素因数分解の利用 問題で 27に整数nをかけて自然数の2乗になるようにしたい。 nをちいさいほうから3つ求めよ。 というものがあったのですが、答えが 3・12・27 となっています。3 質 第2回目は「素因数分解」です。 公務員を目指している方向けに、スーパー過去問ゼミ 数的処理(実務教育出版)にある問題をアレンジし、例題を投稿しています。 レベル1は基本の問題です。 レベル2は国家一般職や地方上級職以上を目指す人向けで、本番で正解してほしい問題です。
4 素因数分解と約数・倍数 ⑴ 次の数の約数をすべて求めなさい。 ① ② 63 ③ 245 〔 〕 〔 〕 〔 〕 ⑵ 102 にできるだけ小さい自然数をかけて,その結果を 70 の倍数にしたい。どんな数をかければよいですか。 〔 〕 5 最大公約数・最小公倍数7.素因数分解の利用(2) 類題 (1)96にできるだけ小さい自然数を掛けて,ある数の2乗にしたい。どのような数をかければよいか。 考え方 どちらも,「96や525に『何か』を掛けたもの」が,ある数の2乗になればよい。毎朝今日の日付(今日で言うと)の素因数分解をしているので、答え合わせに使用しています。 ご意見・ご感想 の素数判定とか計算機なしでどうやるんだ! ? って思いました。 アンケートにご協力頂き有り難うございました。 送信を完了し
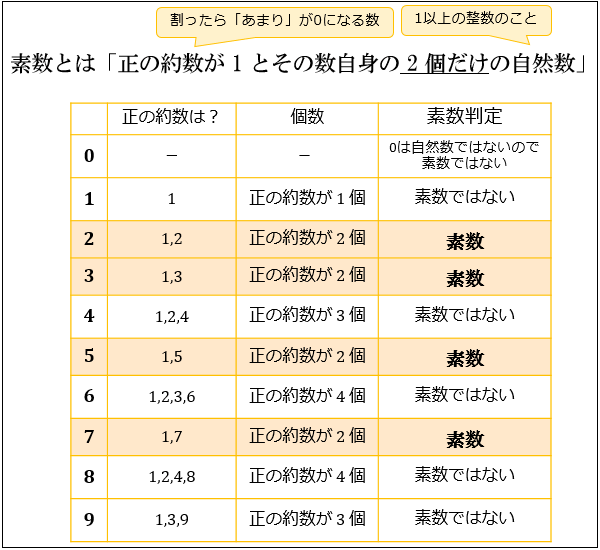
計算力≒素因数分解力普段から僕の生徒さんには,「素因数を意識した計算を!」と言い続けています。具体的には,39 29÷26 110÷165 みたいな感じの×,素因数分解とは、「 素数のかけ算にガンガン分解する 」ことだったね。 ポイントをよく見直しながら、問題を解いて慣れていこう。 まずは 2とか3とか、小さい数で割り切れないかどうか 調べていくの問題 次の素因数分解の問題を解きましょう。 次の数を素因数分解した後に素因数も答えてください。 問1. 9 問2. 18 問3. 25 問4. 39 問5. 60 問6. 100 問7. 0




素因数分解を利用する応用問題の解き方 現役塾講師のわかりやすい中学数学の解き方



素因数分解のドリル
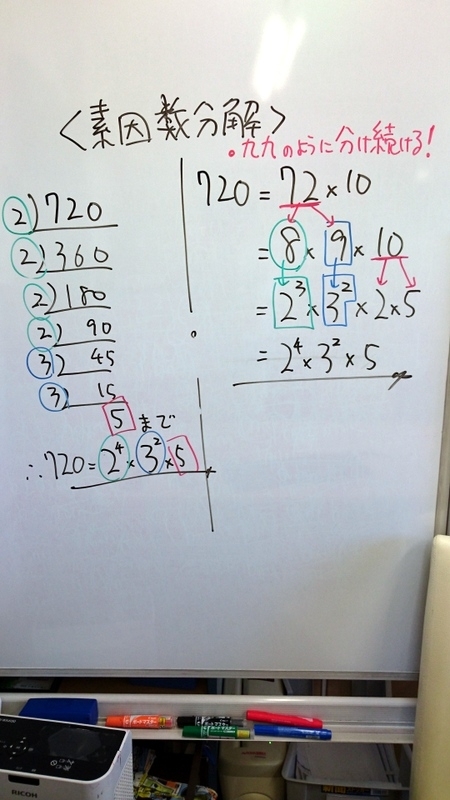
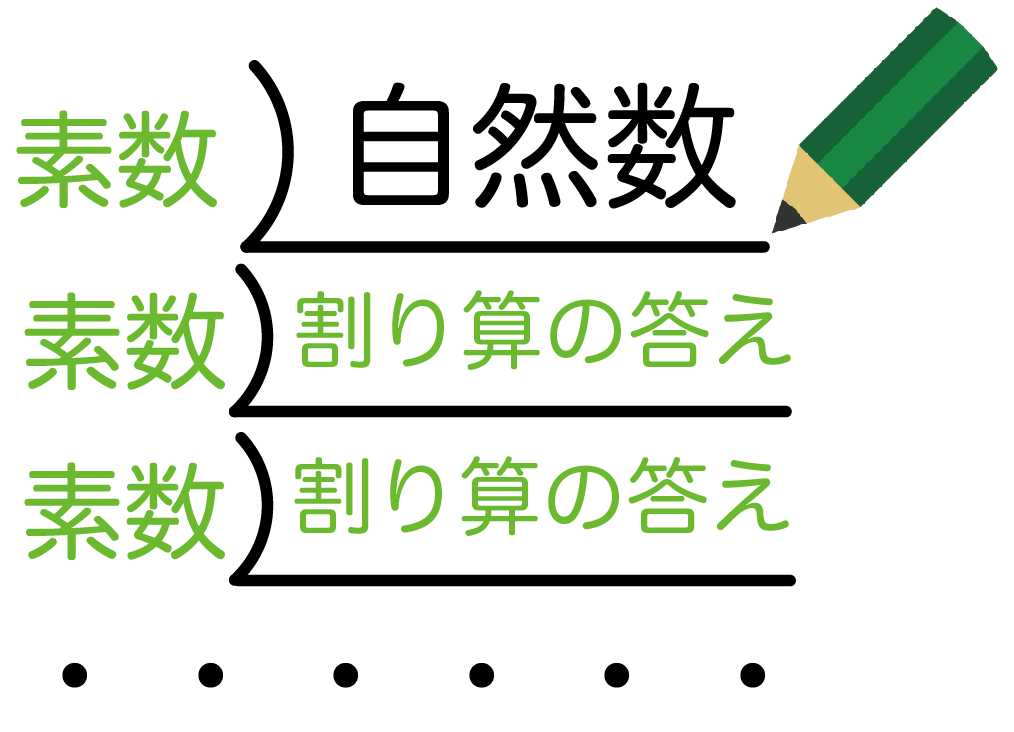
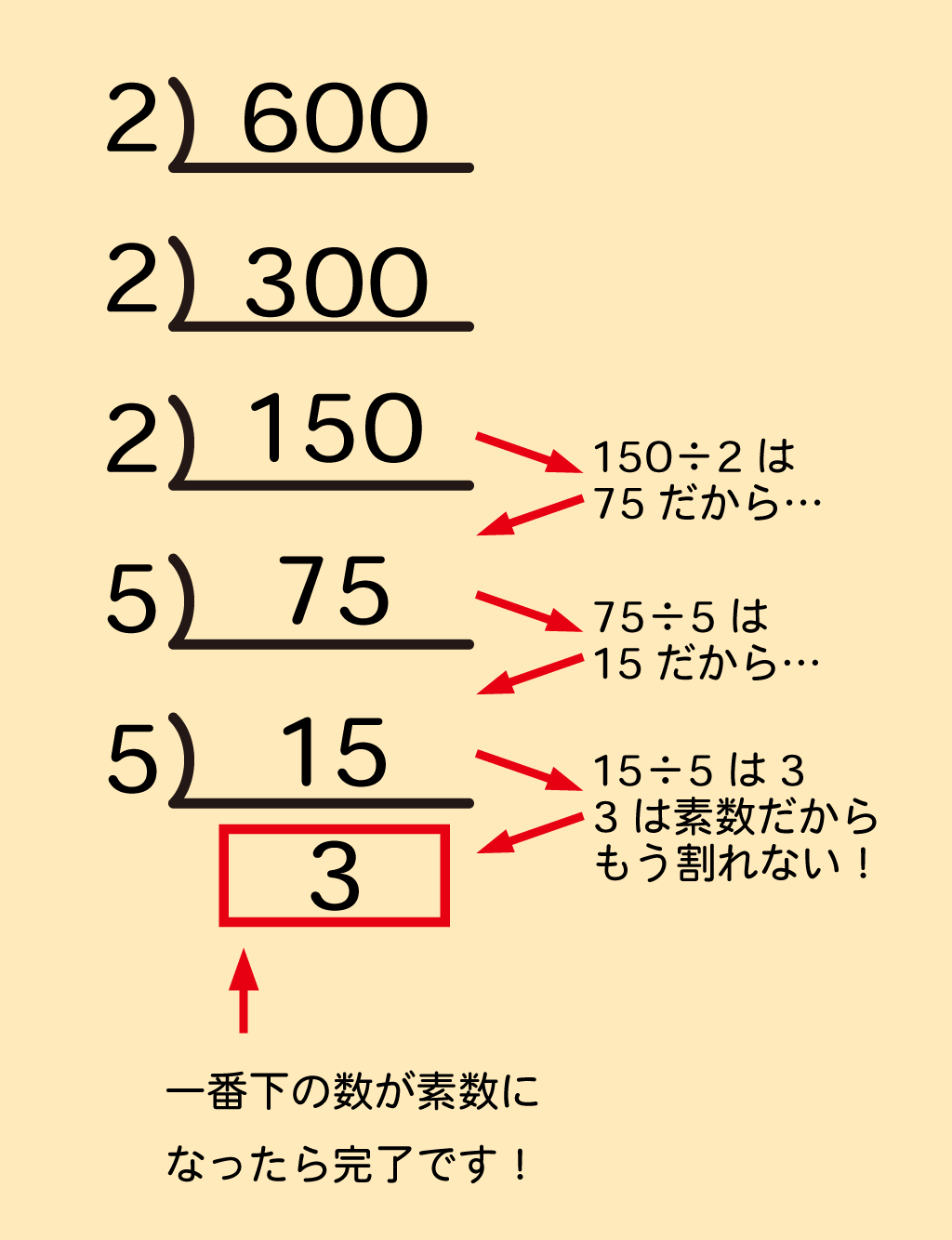
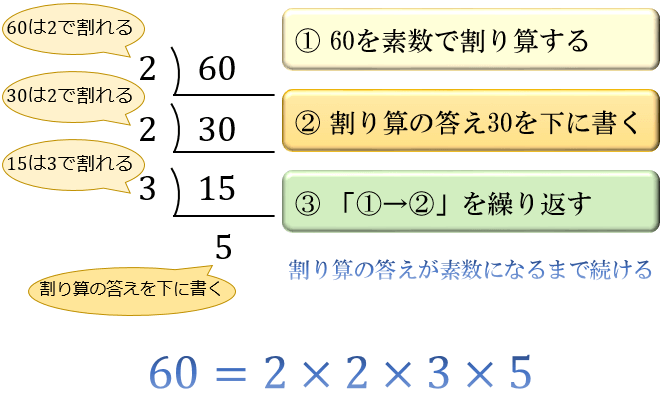
素因数分解をおこなえば、その数字が持つ性質を知ることができます。 は、=2×2×5×101と分解できました。 したがって、は2や5や101の倍数であることが分かります。 では、21を素因数分解するとどうなるでしょうか? 221を素因数分解する方法ある自然数の2乗によってできあがっている数は、素因数分解をするとすべて、 2乗の掛け算によって表すことができる んですね! このことを使いながら問題を解いていきますので、よく覚えておきましょう! 問題の解説! Step① 分解したい数の左下にL字のような記号を書く Step② 分解したい数を素数で割り算する Step③ L字の左に「割った数」、下に「割り算の答え」を書く Step④ 「割り算の答え」が素数になるまで分解しつづける Step⑤ 素数になったら「L字の左側のすべて




数学 中3 5 素数と素因数分解 Youtube



Studydoctor素因数分解の利用 中3数学 Studydoctor
いやいや、この問題素因数分解なんじゃないの?素因数分解使った解法説明してよ。 と思われた方も多いと思います。 そうです、この問題は素因数分解の問題です。 この問題、本来は40を素因数分解し、17の二乗と指数法則を絡めることによって解いていく 数学・算数 素因数分解の問題教えて下さい。 ある整数Nを素因数分解するとN=2^10×3^15×5^10×7^2となった。 この整数Nの正の約数のうち1の位が1であるものは何個あるか求めよ。 と 質問No素因数分解の練習問題 さんが残りますこれは二重ではれているからですね 12ではできるようには 12倍圏にはその素因数分解にかけるにかけるさんでも割り切れなくてはいけませんで これはここは全部消えて 子だけが残りますねということは両方で




中1 1学期 整数の性質 素因数分解 のわかりやすい教え方 教える手順 ノートのとらせ方 問題もあります ワーママhikariの目からウロコ




素因数分解の応用問題の解き方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
素因数分解の難しさと素数判定でも述べたとおり,大きな数の素因数分解は非常に難しいです。難しいながらもできるだけ速い方法を探したいです。 ロー法( ρ \rho ρアルゴリズム)は高確率で短い計算時間で正しい答えを返しますが,失敗することもあり素因数分解計算機 留意事項 自然数を素因数分解してしてくれるプログラムです 入力値は2以上、最大8桁までの自然数に限ります(結構負荷大きので制限かけてます) 素数の場合はその旨判定します 計算 数値を入力して下さい 簡単シンプル! 素因数分解の簡単な方法&計算機 管理人 3月 3, 19 / 2月 18, 21 自然数を素数で因数分解することを『素因数分解』と言います。 素因数分解は小学校のときに約数を調べるのに教わることもありますが、中学校では平方根の計算に使います。 今回は素因




中3 数学 素因数分解 無料学習プリント教材



U9j580gf8iba369ji2w Xyz P 599
という数に関連した問題 という数字そのものに着目してみます。 数字の性質を見るには、素因数分解をしてみることが大切です。 素因数分解は『正の整数を素数の積の形で表す』ことです。 例えば、12=2×2×3となります。 はどうでしょうか。ビデオのトランスクリプト 75の素因数分解を書きなさえ 指数の起用を使って答えを書きなさい 一茶の興味深いことはここにありますねそれは素因数分解と 指数の貴方というものです指数の表についてはあとで考えることにしましょう 最初に考えるとは素因数分解による解法 素因数分解による解法も学習しておきましょう。 \(7=2^4×3^2×5\) 平方数とは、同じ数を \(2\) つかけあわせた数なので \(2,3,5\) という素因数が、偶数個ずつあればよいのです。



素因数分解とは やり方やコツ 利用問題 約数など 受験辞典




ヒントは 素因数分解 にあり 整数問題攻略の大原則を学ぼう まなべーと
3 576 576を素因数分解すると、「2 6 2 」 となる。 2 6 2 = 2 2 2 2 2 2 = 24 2 ≪答≫ 24 4 1296 1296を素因数分解すると、「2 4 4 」 となる。 2 4 4 = 2 2 2 2 2 2 = 36 2 ≪答≫ 36 練習問題5 以下の数にできるだけ小さい自然数Aをかけて、ある整数Bの2乗になるようにスポーツの問題点は素因数分解で解決できる! TIスイム代表の竹内さんにお話を聞いてきた トータル・イマージョン・スイム (以下TIスイム)のジャパン代表である竹内慎司さん。 前編では竹内さんがTIスイムに魅了され、コーチとしてTIスイムを日本へ次の数の平方根を素因数分解を利用して求めなさい。 324 1764 1296 次のようにすでに素因数分解した形で表された数がある。 この①〜③の数について できるだけ小さい自然数をかけてその結果をある整数の平方にしたい。 それぞれ何をかければよいか




中学3年生 数学 因数分解 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
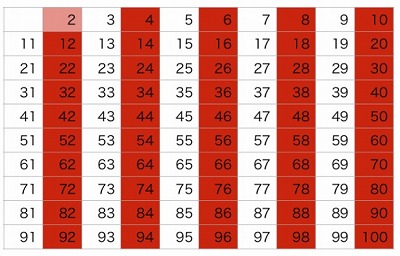



21を素因数分解するといくつ 中学受験算数に出る問題 横浜の学習塾 国大qゼミ
難しく見える問題ですが、素因数分解を利用すると簡単に解くことができます。 まずは、54を素因数分解します。 $$54=2\times 3\times 3\times 3$$ そして、でてきた素因数を2乗のペアにまとめていきます。 $$54=3^2\times 2\times 3$$




素因数分解 問題解答自動作成 授業で使える教材倉庫




高校数学a 素因数分解とは 練習編 映像授業のtry It トライイット




素因数分解とは 素因数分解のやり方を練習問題と解説でマスターしよう 高校生向け受験応援メディア 受験のミカタ




素数 素因数分解の問題です Clear




素因数分解とは 素因数分解のやり方を練習問題と解説でマスターしよう 高校生向け受験応援メディア 受験のミカタ



素因数分解のやり方を分かりやすく解説 計算問題も付いてます Studyplus スタディプラス



3



素因数分解のやり方 5つのステップで分かる素因数分解問題の解き方とコツ アタリマエ



素因数分解のやり方 5つのステップで分かる素因数分解問題の解き方とコツ アタリマエ




素因数分解の応用問題 中学数学 理科 寺子屋塾の復習サイト




ちょっと得する知識シリーズ 1 素因数分解を知れば暗号が分かる 1 Tech



U9j580gf8iba369ji2w Xyz P 1542




素因数分解のやり方のコツとは 応用問題3選も簡単に解けます 遊ぶ数学




中3数学 素因数分解のポイントと定期テスト対策問題 Examee
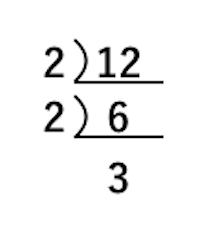



簡単にできる素因数分解 苦手な数学を簡単に



素因数分解とは やり方やコツ 利用問題 約数など 受験辞典




素因数分解 無料で使える中学学習プリント



数学の素因数分解の問題の答え方ですが 弟がこうやって書きました 計算 Yahoo 知恵袋




素因数分解とは 素因数分解のやり方を練習問題と解説でマスターしよう 高校生向け受験応援メディア 受験のミカタ



1 中学時のやり方を捨てよ 7 を10秒で素因数分解する方法 塾講師 加藤哲也 マイベストプロ岐阜



3



素因数分解のやり方を分かりやすく解説 計算問題も付いてます Studyplus スタディプラス




素因数分解の応用問題 中学数学 理科 寺子屋塾の復習サイト



素因数分解をした時の答えの並べ方がわかりません 指数になって Yahoo 知恵袋




中学数学 因数分解 素因数分解のわかりやすい解説 入試問題 数学の面白いこと 役に立つことをまとめたサイト



Studydoctor素因数分解のやり方 中3数学 Studydoctor



素因数分解とは やり方やコツ 利用問題 約数など 受験辞典



素因数分解とは やり方やコツ 利用問題 約数など 受験辞典




素因数分解のやり方 5つのステップで分かる素因数分解問題の解き方とコツ アタリマエ
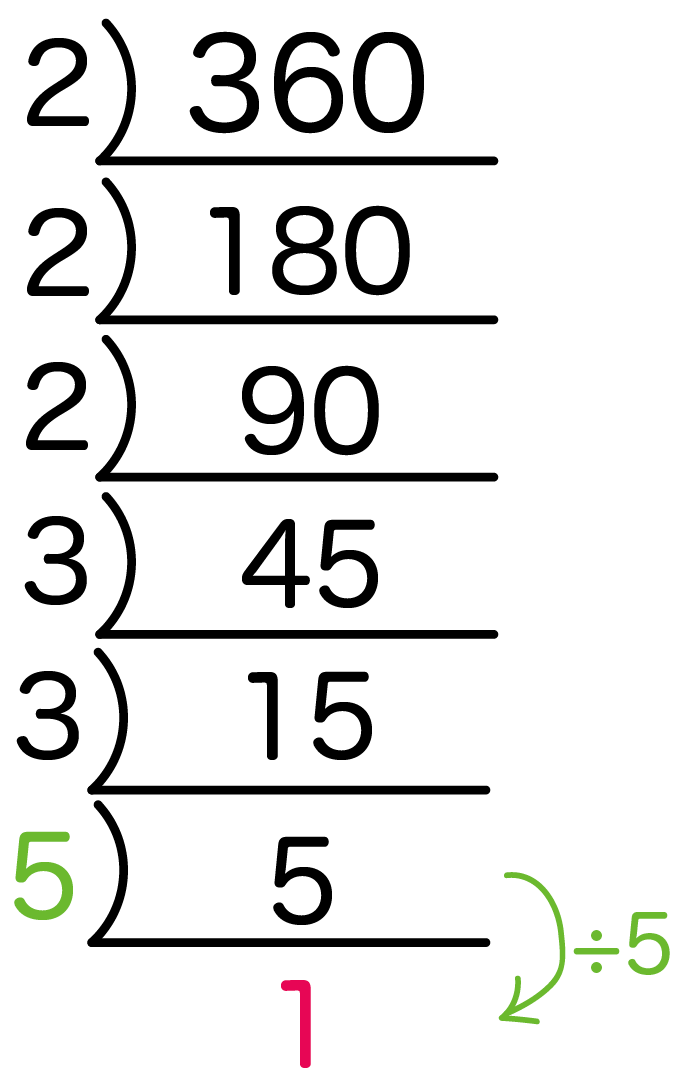



簡単計算 素因数分解のやり方 解き方がわかる5ステップ Qikeru 学びを楽しくわかりやすく
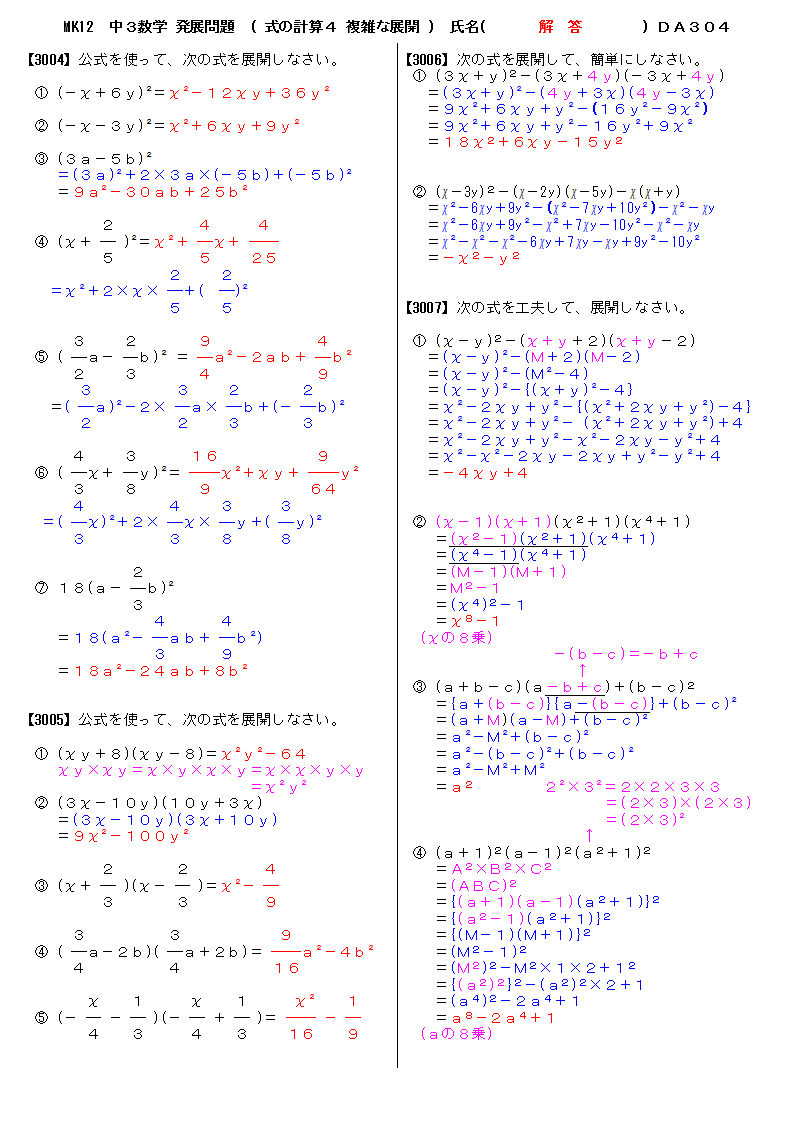



無料 中3数学 発展 応用問題 解答プリント 304 式の計算4 素因数分解




素数 素因数分解の問題です Clear




素因数分解のやり方のコツとは 応用問題3選も簡単に解けます 遊ぶ数学




中学3年生 数学 因数分解 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



簡単計算 素因数分解のやり方 解き方がわかる5ステップ Qikeru 学びを楽しくわかりやすく




素因数分解 第4回 応用問題 ある自然数を2乗すると 1764になります この自然数を求めなさい 中学1年数学内容 Youtube




世界一わかりやすい数学問題集中3 1章 式の展開と因数分解



素因数分解のやり方を分かりやすく解説 計算問題も付いてます Studyplus スタディプラス




素因数分解 無料で使える中学学習プリント



中学数学 因数分解 素因数分解のわかりやすい解説 入試問題 数学の面白いこと 役に立つことをまとめたサイト



3




素因数分解の質問です Clear




素因数分解 ある自然数の2乗になるためには 何をかける わる 数スタ
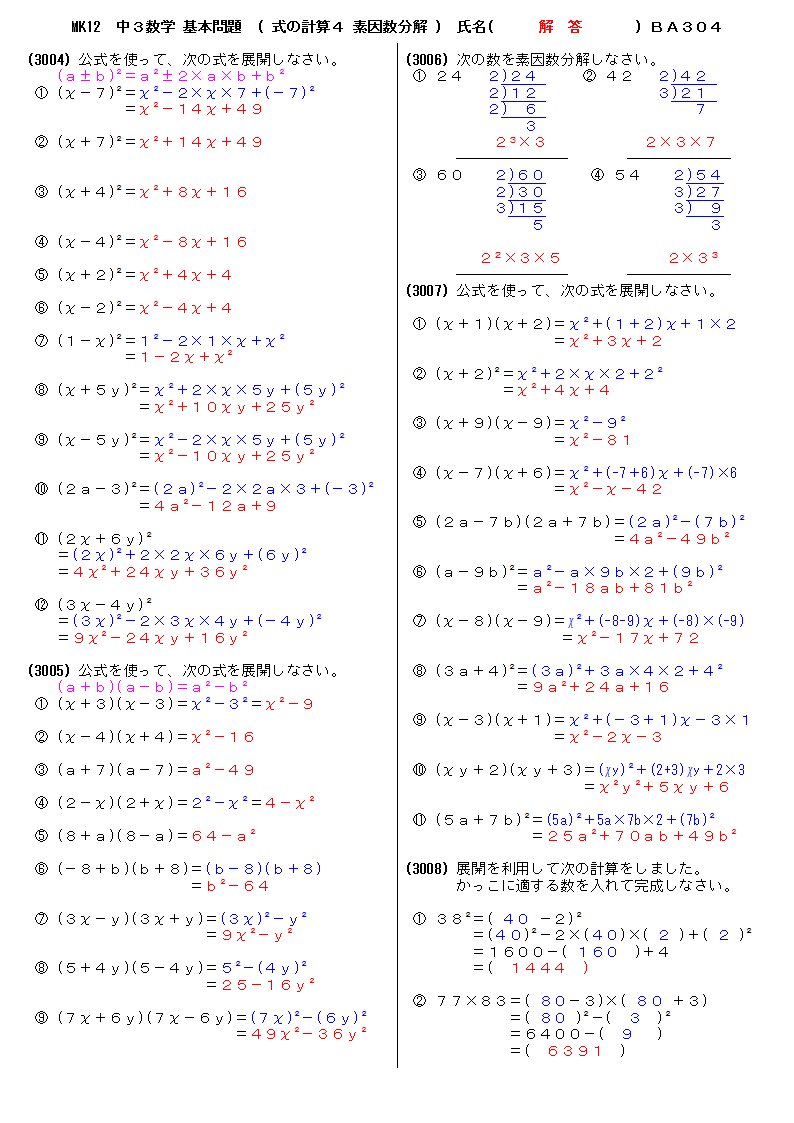



無料 中3数学 基本問題 解答プリント 304 式の計算4 素因数分解



素因数分解のやり方と応用問題の解き方解説



21を素因数分解しょうとすると かなり時間がかかりますよね Yahoo 知恵袋
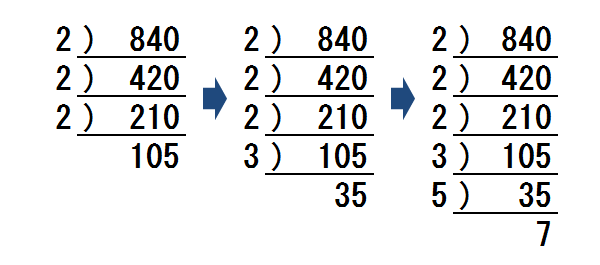



素因数分解のやり方と応用問題の解き方解説




素因数分解のやり方 Youtube



中学3年生向け 平方根はこうやって解く 平方根を基本から徹底解説 学習内容解説ブログ




中3数学 素因数分解とは 練習編 映像授業のtry It トライイット



簡単計算 素因数分解のやり方 解き方がわかる5ステップ Qikeru 学びを楽しくわかりやすく



面白クイズ 9991を素因数分解




素因数分解とは 素因数分解のやり方を練習問題と解説でマスターしよう 高校生向け受験応援メディア 受験のミカタ
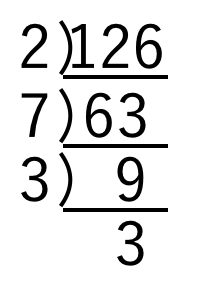



素因数分解を練習する 苦手な数学を簡単に




素因数分解の利用のやり方が分かりません 教えてください このような問題のことです Clear




素因数分解のやり方 簡単な応用問題 数学の偏差値を上げて合格を目指す



素因数分解とは やり方やコツ 利用問題 約数など 受験辞典



U9j580gf8iba369ji2w Xyz P 1542




簡単計算 素因数分解のやり方 解き方がわかる5ステップ Qikeru 学びを楽しくわかりやすく




中3の素因数分解を利用した応用問題なのですが Clear
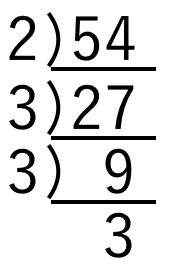



素因数分解を練習する 苦手な数学を簡単に




無料 中3数学 標準問題 解答プリント 304 式の計算4 素因数分解



素因数分解のやり方 5つのステップで分かる素因数分解問題の解き方とコツ アタリマエ




21年度入試予想 21の素因数分解 誘導あり Youtube




素因数分解 第5回 発展問題 54にできるだけ小さい自然数をかけて その積がある自然数の2乗になるようにしたい どんな数をかければよいか答えなさい 中学1年数学内容 Youtube




素因数分解の応用問題の解き方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



素因数分解のやり方を分かりやすく解説 計算問題も付いてます Studyplus スタディプラス




中学数学 因数分解 素因数分解のわかりやすい解説 入試問題 数学の面白いこと 役に立つことをまとめたサイト




問題 素因数分解を利用して 126の約数を求めよ 126 2 3の2乗 7 Clear
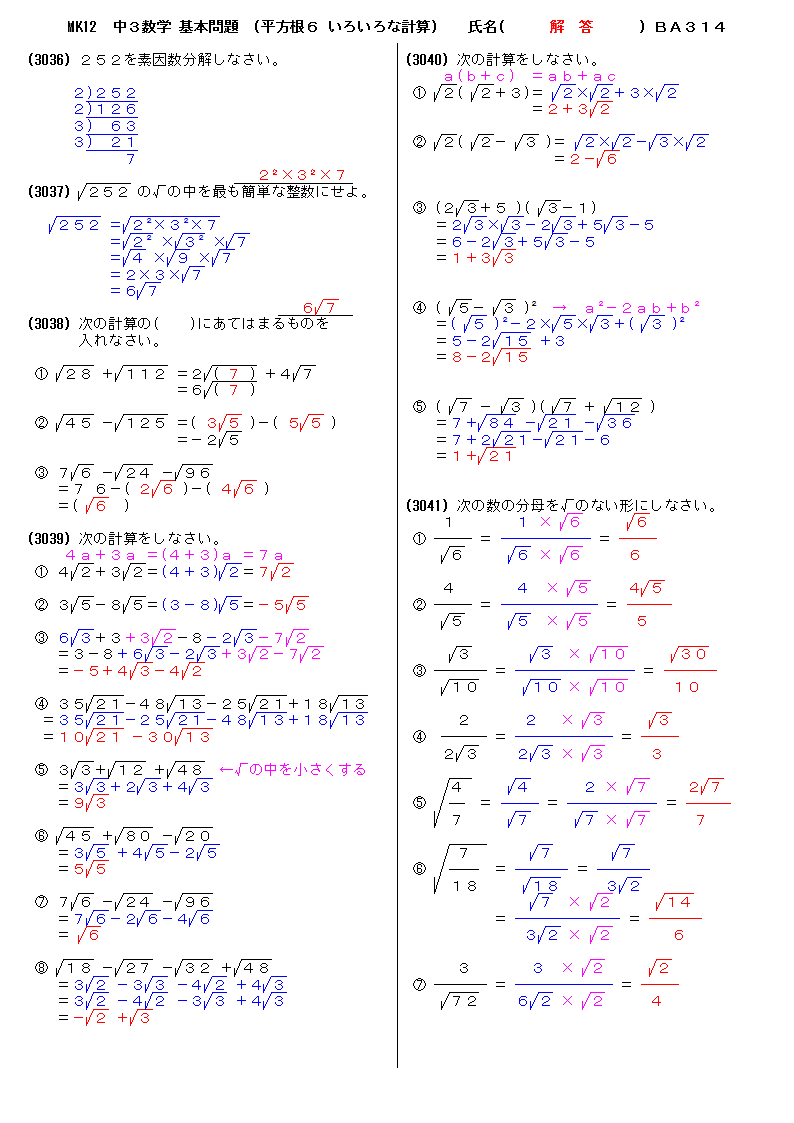



無料 中3数学 基本問題 解答プリント 314 平方根6 いろいろな計算
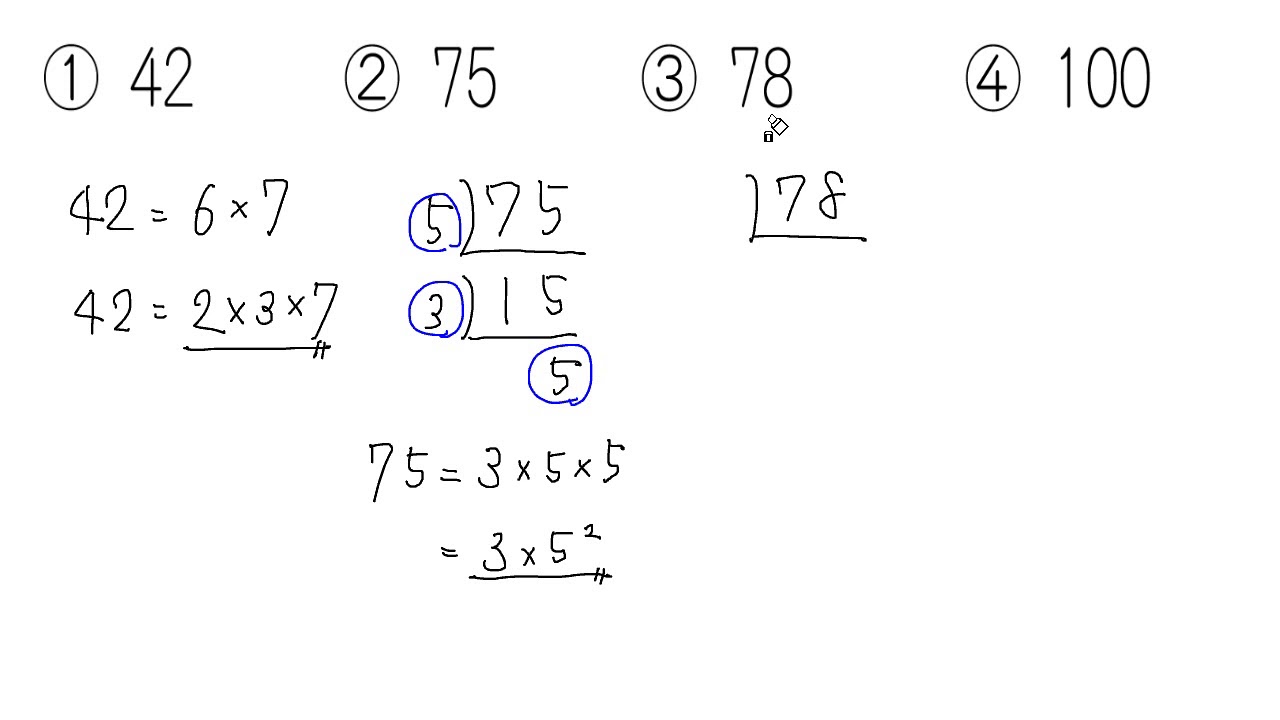



素因数分解 問題 Youtube




約数の個数の求め方 素因数分解すれば一発で求まる 高校生向け受験応援メディア 受験のミカタ




天才ドリル 素因数パズル 小学校3年生以上 算数 考える力を育てる 認知工学 本 通販 Amazon




素因数分解の利用問題なのですが 2が4乗されているのはそのままで良い のがよくわかり Clear




因数分解 これが解けたらすごいよ 苦手な数学を簡単に




中学数学 因数分解 素因数分解のわかりやすい解説 入試問題 数学の面白いこと 役に立つことをまとめたサイト
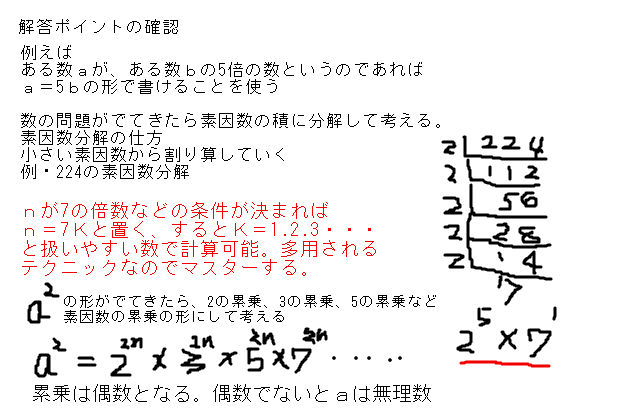



素因数分解の応用問題 中学数学 理科 寺子屋塾の復習サイト




素因数分解とは やり方をイチから解説 Youtube




素因数分解とは 素因数分解のやり方を練習問題と解説でマスターしよう 高校生向け受験応援メディア 受験のミカタ




中学数学 因数分解 素因数分解のわかりやすい解説 入試問題 数学の面白いこと 役に立つことをまとめたサイト



Search Q 21 E7 B4 A0 E5 9b A0 E6 95 B0 E5 86 E8 A3 Tbm Isch



中学数学 平方根 のコツ 素因数分解 ルートを簡単にする計算




素因数分解とは 素因数分解のやり方を練習問題と解説でマスターしよう 高校生向け受験応援メディア 受験のミカタ



数学の素因数分解の問題なのですが 答えはこれであっていますか 最後 Yahoo 知恵袋



素因数分解とは やり方やコツ 利用問題 約数など 受験辞典




ม 3 โน ตของ 中3数学 式の計算 素因数分解と因数分解 ช น Clear




中学3年生向け 平方根はこうやって解く 平方根を基本から徹底解説 学習内容解説ブログ




素因数分解 無料で使える中学学習プリント



素因数分解のやり方を分かりやすく解説 計算問題も付いてます Studyplus スタディプラス




中3 数学 素因数分解 この問題の解説をお願いします なぜ よって の Okwave




100 を素因数分解すると2 A 3 B 5 C 7 16 11 9 13 7 とな Clear
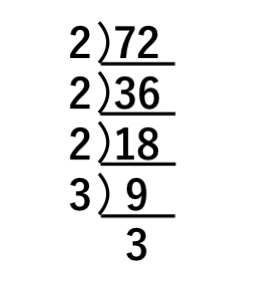



簡単にできる素因数分解 苦手な数学を簡単に



0 件のコメント:
コメントを投稿