A = 面積 P = 円周(近似式) 円錐 V = 体積 A = 円錐面積 r = d/2 = 半径 三角錐 V = 体積 S = 角錐底面積 角錐 角錐 pyramid V = 体積 S = 角錐底面積 角錐台 V = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積 球体 V = 体積 A = 球体の表面積 r = 球体半径 円錐の表面積は、母線×底面の半径×π+底面積なので、12×(10÷2)πで求められます。 なので側面積は、60π㎠です。 底面積は10÷2πなので5π㎠です。 したがって、表面積は(60+5)πで65π㎠です。1 円錐曲線 円・楕円・放物線・双曲線は,何れも二次曲線であり,円錐曲線の仲間である.円錐曲線(conic section) は,下図に示す通り,円錐形をまっすぐ切った切り口の形である.例えば,円錐形の軸に対 して直角に切ると,切り口は円形となり,母線に対して平行に切ると,切り口は放物線と

円錐の表面積の求め方 公式と計算例
円錐 形 表面積
円錐 形 表面積-表面積を求める方法! 母線を使った裏ワザ公式とは!? 円錐の表面積、中心角 まとめ 中3受験生へこの力を身につけたら本番で60点は楽勝にとれる! こちらの関連記事はいかがでしょうか?S = πr2 πrl = πr2 πr√r2 h2 S = π r 2 π r l = π r 2 π r r 2 h 2 表面積 = 半径 × 半径 × 314 半径 × 母線の長さ × 314 公式の導出方法と計算例については、「 円錐の表面積の求め方 」をご覧く




円錐の表面積の求め方 公式と計算例
6cm 表面積=4π×6×6=144π(cm 2) 体積= 4 3 π×6×6×6=2π(cm 3) 回転体の体積 回転体は、円錐や円柱、球などの組み合わせでできているので、 それぞれの部分で体積を出して足したり、引いたりする。 (例1) l 図A l 図B 円柱 円錐 半球 図Aを直線lを軸に一回転させると円錐の表 == 立体の表面積(円柱,角柱,円錐,角錐の表面積) == 解説 立体の表面積は「展開図」で考えるとよく分かります。 右図アの立方体(正四角柱で縦横高さとも同じもの)の表面積 10×10=100(cm 2)の正方形が6個あるから 600(cm 2)・・・答 この図は、円錐を円錐は、錐体の一種である。 高さを h、母線の長さを c、底面の半径を r、底面積を B (= π r 2)、底面の周を b (= 2 π r)、 と置けば、円錐の側面積 S side 、表面積 S、体積 V はそれぞれ以下で与えられる : = = = = = () = () = = = 標準化 円錐面は、適当な直交変換を行うことにより、次の陰関数に
半径2 = 62 −(4√2)2 = 36 −32 = 4 半 径 2 = 6 2 − ( 4 2) 2 = 36 − 32 = 4 ∴ 半径 = 2 半 径 = 2 (半径 > 0 より) これで、 この図になって、これは 最初の問題と同じ だね だから、中心角は1°! はかせちゃん 円錐って英語でcone (コーン)らしいんだけど、 とんがり円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学 > 図形 > 円錐台の体積と表面積を計算する公式と証明 最終更新日 図のような円錐台について、 体積は、 V = 1 3 π h ( a 2 a b b 2) 側面積は、 S L = π ( a b) ( a − b) 2 h 2 表面積は、 S側面 (長方形)・・・h×2πr = 2πhr 表面積・・・2πr 2 2πhr
・正方形や円などの面積,直方体の体積の求め方を 黒板にまとめておくとよい。 ・様々な柱体と錐体を見せ,円柱,円錐など名称を 言わせる。 展 開 1 ②円柱と円錐,四 角柱と四角錐の 体積の関係から, 同じ底面積で同 じ高さをもつ他 の立体(五角柱と 中1数学「立体の表面積」の問題 どこよりも簡単な解き方・求め方 kazunokazu 21年8月5日 宿題かんたんにできるかな?』円すいの表面積 次の図形の表面積を求めましょう。 問題集の無料ダウンロードサイトは「おかわりドリル」で検索 https//wwwokadorinet ©おかわりドリル ① 2cm 4cm 5cm 4cm ② ③ 6cm 4cm 1cm 底面積は2×2×π=4π 側面のおうぎ形の弧



計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




数学でどうしてもわからない問題があります この円錐の表面積を求め 中学校 教えて Goo
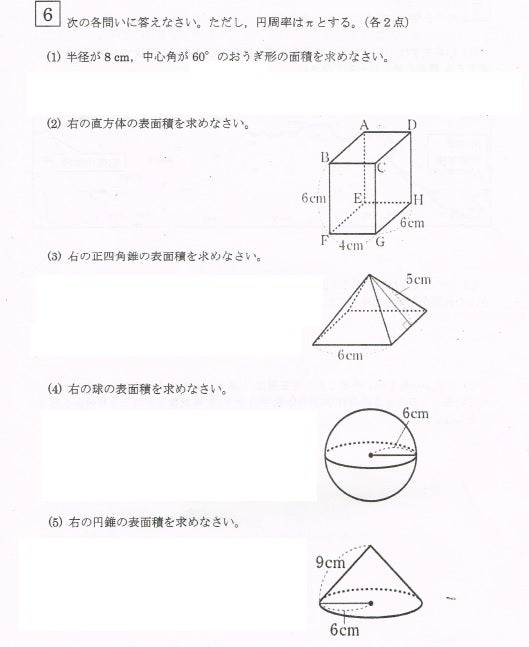
7 立体の体積と表面積 143 右の図の円錐について,次の問いに答えよ。 ⑴ 底面積を求めよ。 ⑵ 側面の扇形の中心角を求めよ。 ⑶ 側面積を求めよ。 ⑷ 表面積を求めよ。 学基本学習の基本 34 円錐の体積と表面積 問題1 右の図の円錐の体積を求めよ。_1_幾何I_本冊2章smd Page 19 17 v340 166 次の図の立体の体積と表面積を求めよ。 ⑴ ⑵ ⑶ 167 右の図は,直方体から円柱の半分を切り取った立体である。 この 立体の体積と表面積を求めよ。 168 右の図は,縦6cm,横8cmの長方形から,1辺4cmの正方形を円柱の表面積の解説 円柱の表面積を求めるには、まず上下の円の部分と側面の部分を分けて考えます。側面部分は筒状ですが、開いて四角形の状態にします。 円の面積は 半径×半径×円周率 なので、上下の円の面積を求めます。側面部分は四角形なので 縦



円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学



円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学
円錐の体積=底面積×高さ÷3なので 答え 096cm³ スポンサードリンク 問題③ 体積が1570cm³である次の円錐の高さを求めましょう。 (円周率は314とします。) 《円錐の高さの求め方》 円錐の体積=底面積×円錐の高さ÷3であることから これで展開図の長方形のよこの長さがわかり、求めたい円柱の側面積がわかりますね。 底面の円周(長方形のよこの長さ)は 2×3×π=6π cm 円柱の側面積は 8×6π=48π cm 2 底面積は 3×3×π=9π cm 2高評価 4,027件 再生 118,739回 公開日 年11月25日




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ




立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学
円錐の表面積 底面の半径が r ,母線の長さが R の円錐の表面積を求めるには,右図のように展開図で考え,底面積=円と側面積=扇形の面積を各々求めて加えるとよい. 底面は半径 r の円だから,その面積は πr 2 (1) 側面の扇形の面積を求めるためには,その中心角を求めることが重要に 底面 半径 600 高さ 300の円錐形です。 底面の中心から水平方向に150離れた線で、高さ方向に垂直に切り取ります。 切り取られた立体の側表面積を教えてください。 できるだけ簡潔に、 立体の表面積を求める問題です。 考え方のポイント 立体の表面積は展開図を書いて考えましょう。 例)立方体は正方形が6枚 正方形の面積×6 *展開図が頭に思い浮かぶ場合は直接求めて構いませんが、よく分からない場合は自分で展開図を書いて長さを書いていくようにしてください。




3d100 Descubre Como Resolverlo En Qanda




計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
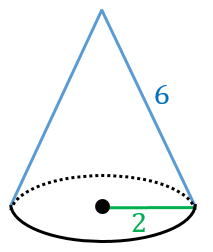
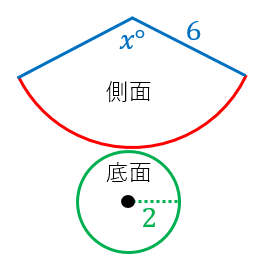
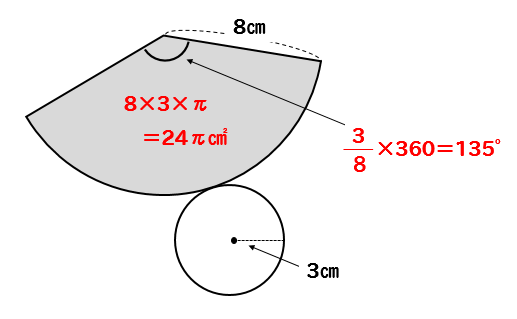
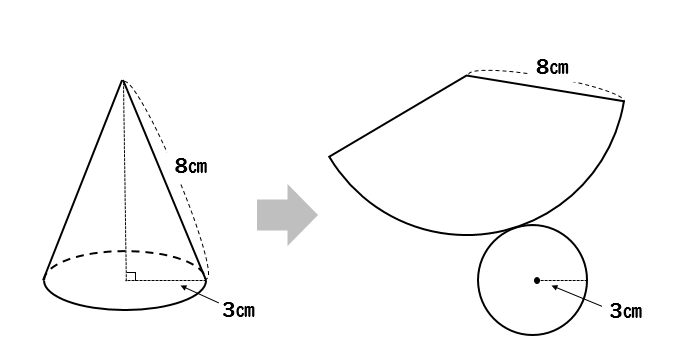
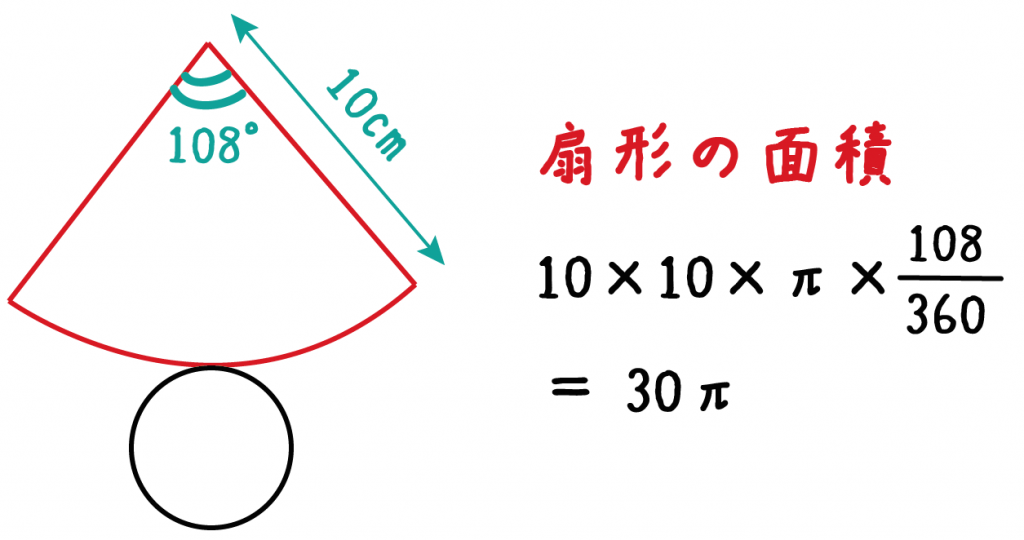
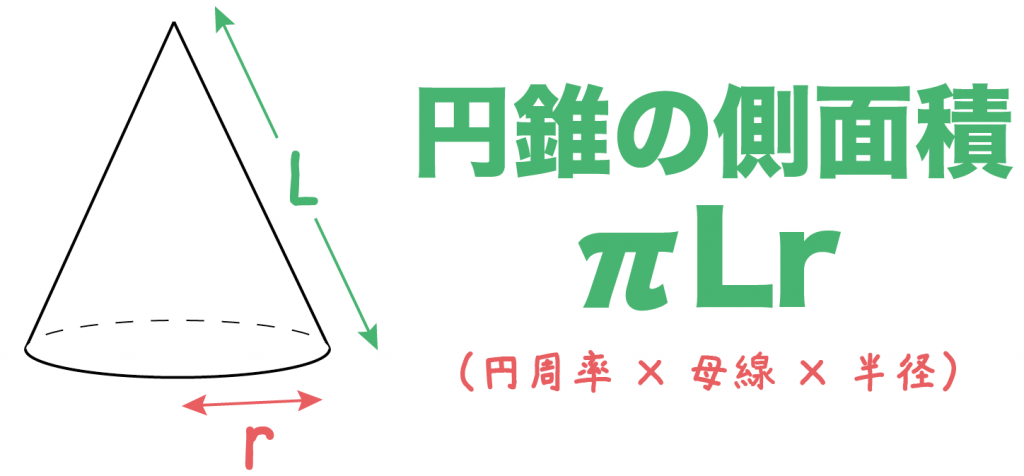
S:球の表面積ってどうやって求めるのだろう。 s:円の場合は細かな三角形に分割して面積を求めたよ。 円錐の側面積も三角形に分けると簡単に求めることがでる。球でも、同じじゃないかな。 s:そういえば、地球儀を作る時に細かな三角形を張り合わせるでしょう。 円錐の側面積を求める公式より、 円錐の側面積 = 母線 × 半径 × 円周率 = 8cm × 3cm × π = 24 π cm 2 扇形の面積を求める公式を導出する 円錐の側面積 = LRπ で求めることができることがわかりましたが、この式を変形してみます。角錐・円錐の表面積 解説 角錐や円錐は,底面が1つなので, (角錐・円錐の表面積)=(底面積)(側面積) という計算で表面積を求めることができますが,表面積は「表面全体の面積」であるので,表面全体がわかりやすいように,見取り図から展開



1



円錐の表面積 中心角を求める問題を丁寧に解説 数スタ
側面積=母線×半径×π =9×3×π =27π (㎠) 表面積=9π+27π =36π (㎠) 以上です! めちゃくちゃ簡単じゃないですか? 以上のように、、「円錐の表面積」の問題は 公式1つでとても簡単になります。 それでは今すぐ上の円錐の表面積を側面積=母線×半径×π =9×次に、円すいの側面積の公式を導きましょう。 円すいの側面積は、半径が母線のおうぎ形なので、 側面積 = 母線×母線×π× x 360 側 面 積 = 母 線 × 母 線 × π × x 360 ですが、 x 360 = 底面の半径 母線 x 360 = 底 面 の 半 径 母 線 でしたので、これを代入する q 底面の半径が3㎝、高さが6㎝の円錐aがあり、この 円錐aと体積が等しい円柱bがある。 円柱bの底面の半径が 3㎝のとき、円柱bの表面積を求めなさい。 (問題文の下に円錐aの図が書いて



Math 円錐の側面積が1秒で求められる公式 中学生 働きアリ




円錐の表面積のやり方を忘れてしまいました 1問でも良いのでお願いします Clear
Keisanより 長径a,短径bの楕円の面積S=πab、半径rの円の面積はS=πr 2 ですので、直円錐の体積の半径rに開平√ (a*b)を計算して代入すれば、楕円錐の体積が求まります。 5 2338 男 / 歳未満 / 学生 / 役に立った / 使用目的 これからの数学との戦い ご動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru円錐の表面積の求め方概要 底面積を求める 扇形の面積を求める 底面積と扇形の面積を足し合わせる こんな感じ! 展開して考える っていうのがポイントだよ じゃあ、さっそくやっていこう! 問題 今回の問題はこちら 底面積を求める




立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学




中学数学 円すいの表面積 中学数学の無料オンライン学習サイトchu Su
円錐台の体積 110 /138件 表示件数 5 10 30 50 100 0 1 1632 男 / 歳未満 / 会社員・公務員 / 非常に役に立った / 使用目的 拡底杭の拡底部の計算 ご意見・ご感想 拡底部の円錐台状の箇所に入れるコンクリート量を計算しました。図の円錐は底面の半径が5cm,表面積が60πcm 2 である。この円錐の母線の長さを求めよ。 右の図のサッカーボールは、12個の正五角形と個の正六角形の合わせて32面でできた多面体である。どの頂点にも1個の正五角形と2個の正六角形の面が集まっている。




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ




中学数学 円錐の高さの求め方 頻出パターン なぜか分かる はかせちゃんの怪しい研究室




角錐 円錐の体積と表面積の公式 数学fun




円錐の表面積を 公式を使って求める チーム エン
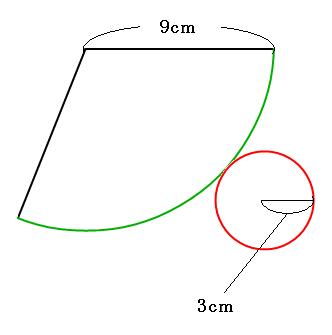



円錐の表面積の求め方を解説 円錐の表面積の求め方は完全パターン化できる




角錐 円錐の体積と表面積の公式 数学fun




中1数学 円すいの問題 練習編 映像授業のtry It トライイット




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ
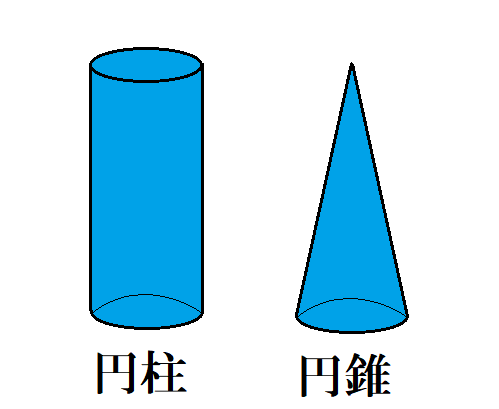



円柱と円錐の違い 表面積や体積 展開図など調べてみたよ ヒデオの情報管理部屋




円錐の表面積の求め方 公式と計算例
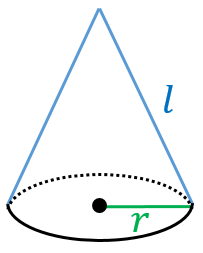



円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学




計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



円錐とは 体積 表面積の公式や求め方 受験辞典




立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学




6 1 5 Cm4 Cm3 Cm 2 3 Descubre Como Resolverlo En Qanda




円錐の側面積 展開図の扇形の中心角 教科書から 身勝手な主張



円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者




中1数学 円柱 円すいの表面積の求め方がサクッとわかる 映像授業のtry It トライイット




19年前期 千葉県公立高校入試 数学 第5問 文章題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト




公式を図解 すい体の体積 円すいの表面積の求め方




毎日問題を解こう 27 苦手な数学を簡単に




角錐 円錐の体積と表面積の求め方 錐体の公式と母線の概念 リョースケ大学



図の円錐の展開図で おうぎ形と半径は4cm 中心角は90 である この展開 Yahoo 知恵袋




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ




公式を図解 すい体の体積 円すいの表面積の求め方




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




円錐の表面積の求め方 公式と計算例



球の半分と円錐を組み合わせた立体です 体積と表面積を求めよ 教え Yahoo 知恵袋



円錐の表面積 中心角を求める問題を丁寧に解説 数スタ




公式を図解 すい体の体積 円すいの表面積の求め方




円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者




中1数学 円柱 円すいの表面積の求め方がサクッとわかる 映像授業のtry It トライイット




中学数学 円錐の裏技集 暗算で中心角 側面積 表面積 中1数学 Youtube




計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




どうしてこのような解説になるのですか Clear




中1数学 円柱 円すいの表面積の求め方がサクッとわかる 映像授業のtry It トライイット



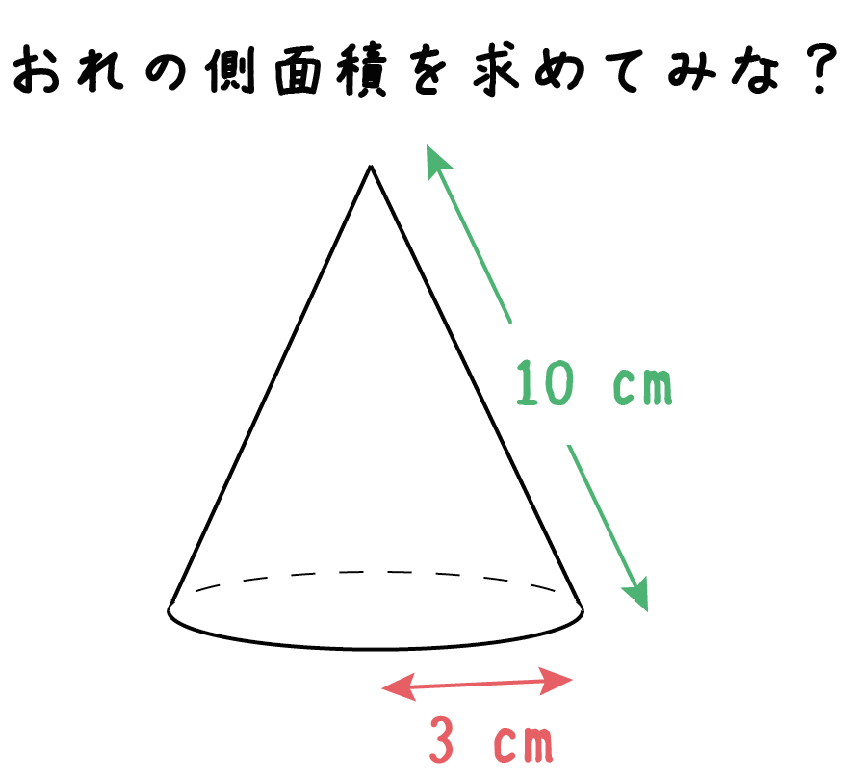
簡単公式 円錐の側面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



円と球 おうぎ形と円すい セルモ大蔵 世田谷 の塾長ブログ




中1数学 円柱 円すいの表面積の求め方がサクッとわかる 映像授業のtry It トライイット




計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




中学数学 円錐の表面積の求め方と公式 図たくさん なぜか分かる はかせちゃんの怪しい研究室




円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学



簡単公式 円錐の側面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




円錐の体積ってなんであの公式なの Webty Staff Blog




円錐の表面積の求め方 You Look Too Cool



簡単公式 円錐の側面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
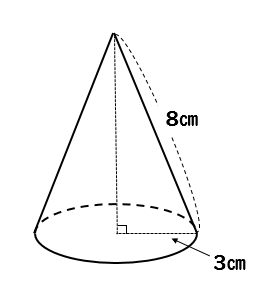



円錐の表面積 中心角を求める問題を丁寧に解説 数スタ



円錐とは 体積 表面積の公式や求め方 受験辞典




中1 回転体の表面積と体積についてです 右の画像が模範解答です Clear




円錐の表面積 あんず学習塾のメモ 図表置き場



円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者



1




裏ワザ公式 円すいの側面積を一瞬で求める方法 Youtube




円錐の表面積 中心角を求める問題を丁寧に解説 数スタ




角錐 円錐の体積と表面積の求め方 錐体の公式と母線の概念 リョースケ大学
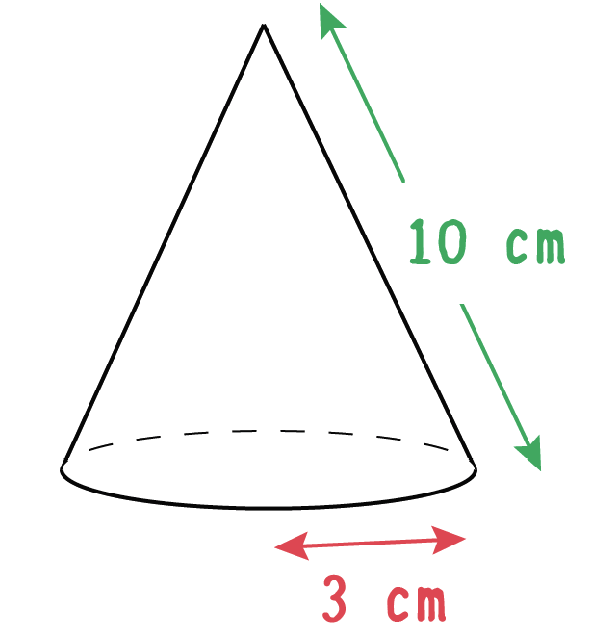



計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




90 4cm 90 Descubre Como Resolverlo En Qanda
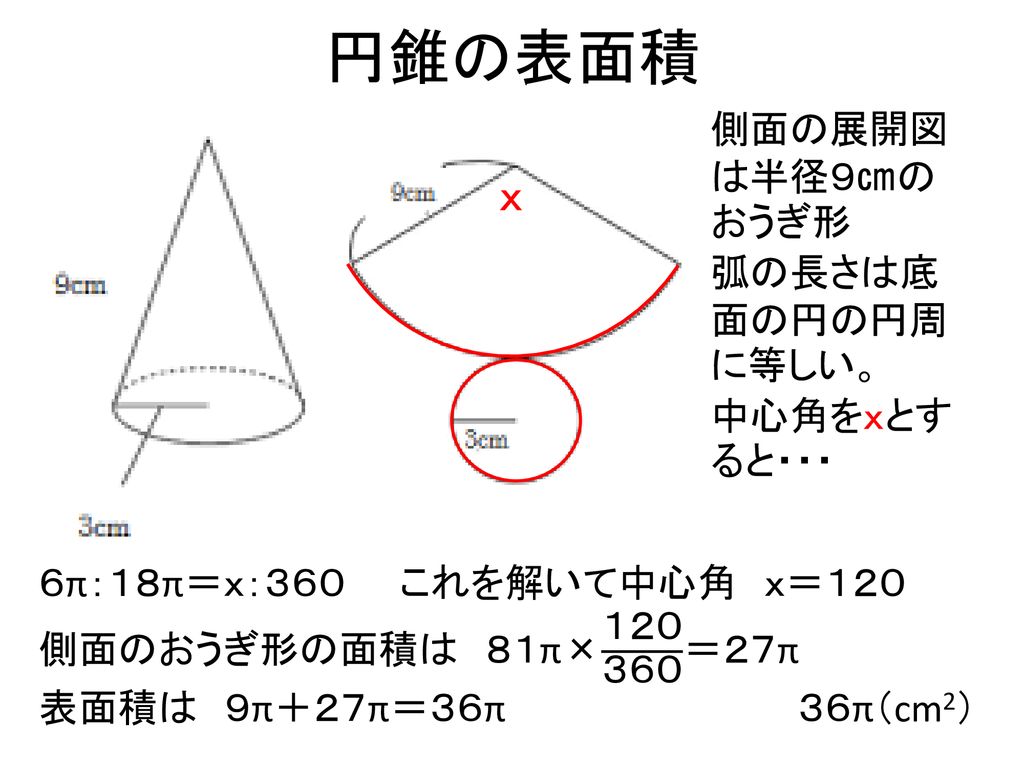



本時の目標 いろいろな立体の表面積を求めることができる Ppt Download
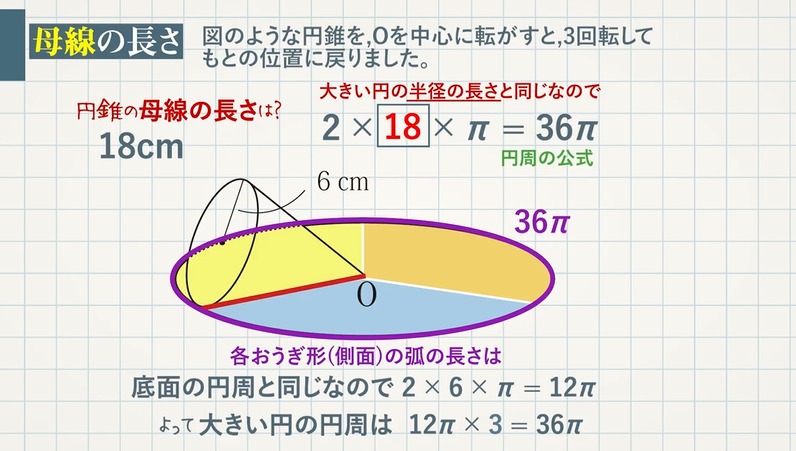



円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者



円錐とは 体積 表面積の公式や求め方 受験辞典



双円錐 Wikipedia




計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




円錐の体積と表面積の求め方 押さえておくべき公式と解法の手順



1




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット




角錐 円錐の体積と表面積の公式 数学fun




角錐 円錐の体積と表面積の公式 数学fun




円錐の表面積 中心角を求める問題を丁寧に解説 数スタ




中1 回転体の表面積と体積についてです 右の画像が模範解答です Clear



1



円錐の体積と表面積の求め方を教えてください 錐の体積 1 Yahoo 知恵袋




公式を図解 すい体の体積 円すいの表面積の求め方




1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




円錐の母線 半径 中心角の関係式とそれぞれの求め方 具体例で学ぶ数学




円錐の表面積 Youtube




円錐の表面積 Youtube




Math 円錐の側面積が1秒で求められる公式 中学生 働きアリ




円錐の表面積の求め方 裏技の公式を覚えたらめちゃくちゃ簡単 中学や高校の数学の計算問題




中学1年生 数学 無料問題集 円すいの表面積 おかわりドリル




角錐 円錐の体積と表面積の公式 数学fun




円錐の体積の公式 死ぬほど問題に出るので求め方を絶対に覚えよう 中学や高校の数学の計算問題




円錐の表面積の求め方を解説 円錐の表面積の求め方は完全パターン化できる



円錐とは 体積 表面積の公式や求め方 受験辞典




円すいの展開図 表面積の求め方 公式があるの知っていますか




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ




2 の円錐の側面積の式の意味が分かりません Clear




円錐の表面積 あんず学習塾のメモ 図表置き場
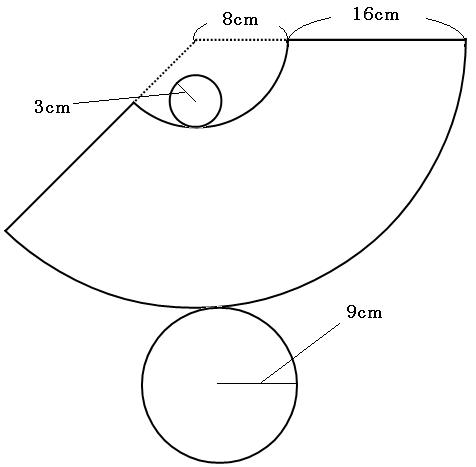



円錐の表面積の求め方を解説 円錐の表面積の求め方は完全パターン化できる




中3 三角形の相似 円錐の体積比 日本語版 Youtube



0 件のコメント:
コメントを投稿