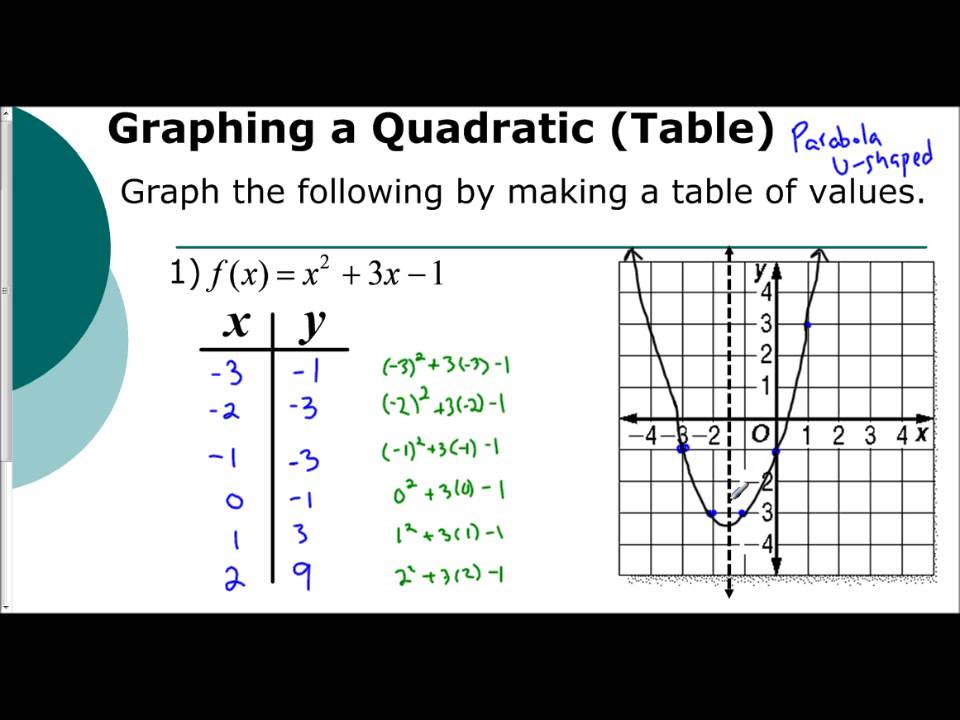
Example 3) Graph y = x 2 4x 7 a = 1, b = 4, and c = 7 Since a 0 the parabola opens up (is U shaped) To find the x intercept we plug in 0 for y 0 = x 2 4x 7 (this expression does not factor so we have to use the quadratic formula) Since the roots are imaginary the parabola has no xintercepts We find the yintercepts by pluggingParabola Opens Right Standard equation of a parabola that opens right and symmetric about xaxis with vertex at origin y 2 = 4ax Standard equation of a parabola that opens up and symmetric about xaxis with at vertex (h, k) (y k) 2 = 4a(x h) Graph of y 2 = 4axClick on the intersection of the x axis and the graph of the parabola to check your solutions
The Parabola Below Is A Graph Of The Equation Y X 1 2 3 Mathskey Com
Graph the parabola y=x^2-4x+3
Graph the parabola y=x^2-4x+3-How to Graph a Parabola of the Form {eq}y=x^2 bx c {/eq} Example 2 This time we won't have an initial graph to guide us! The curve y 2 = x represents a parabola rotated 90° to the right We actually have 2 functions, y = √ x (the top half of the parabola);



Understand How The Graph Of A Parabola Is Related To Its Quadratic Function College Algebra
Question I do not know how to graph the parabola y= x^2 Found 2 solutions by stanbon, jim_thompson5910 Answer by stanbon(757) (Show Source) You can put this solution on YOUR website! The plot can be obtained by reflecting the function y=x^2/2 about the 45degree line All the previous answers (PSTricks, MetaPost, TikZ) use a plot to draw the parabola So they use a lot of segments to approximate it In the spirit of this answer I want to advocate to use a single quadratic (cubic) curve to draw the exact parabola For a quadratic of the form x = ay2 by c, the axis is a line that passes through the vertex and is parallel to the y axis For our parabola, the axis is the line #y = 2 It's not part of the parabola itself, but lightly marking this line on your graph can help you see how the parabola curves symmetrically Step 5
The graph of a quadratic function is a Ushaped curve called a parabolaOne important feature of the graph is that it has an extreme point, called the vertexIf the parabola opens up, the vertex represents the lowest point on the graph, or the minimum value of the quadratic function If the parabola opens down, the vertex represents the highest point on the graph, or the maximumThe "general" form of a parabola's equation is the one you're used to, y = ax 2 bx c — unless the quadratic is "sideways", in which case the equation will look something like x = ay 2 by c The important difference in the two equations is in which variable is squared for regular (vertical) parabolas, the x part is squared; The beginning of an indepth study of graphing quadratic equations (parabolas) Includes the vocab words vertex and axis of symmetry
The Graph of a Quadratic Equation We know that any linear equation with two variables can be written in the form y = mx b and that its graph is a line In this section, we will see that any quadratic equation of the form y = ax2 bx c has a curved graph called a parabolaArrange the equation in the vertex form, Y = a(X h)^2 k or general form Y=aX^2bXc The equation is already written in general form Find the vertex by formula for X coordinate X = b/2a and then plugging the value of X in the equatioThe graph of mathy^2=ax/math will be parabola Two graphs are shown below for positive and negative values of matha=1/math matha=1/math matha=1/math



How To Draw Y 2 X 2 Interactive Mathematics




Graph Of An Equation
I do not know how to graph the parabola y= x^2 Plot a few points and draw a smooth curve thru themAnd y = −√ x (the bottom half of the parabola)Free Parabola calculator Calculate parabola foci, vertices, axis and directrix stepbystep View interactive graph > Examples vertices\x=y^2;




Find The Area Of The Region In The Xy Plane Enclosed By Two Parabolas Y X 2 And Y 2x X 2 Socratic



Lesson 5 1 Introduction To Graphing Parabolas Tables Youtube
Graph a parabola by finding the vertex and using the line of symmetry and the yinterceptA p arabola is a curve and whose equation is in the form of f (x) = ax2bxc, which is the standard form of a parabola To draw a parabola graph, we have to first find the vertex for the given equation This can be done by using x=b/2a and y = f (b/2a)Select a few x x values, and plug them into the equation to find the corresponding y y values The x x values should be selected around the vertex Tap for more steps Substitute the x x value − 2 2 into f ( x) = √ − x f ( x) = x In this case, the point is ( − 2, ) ( 2, )



Graph Equation Of Circle And Parabolas Step By Step Math Problem Solver
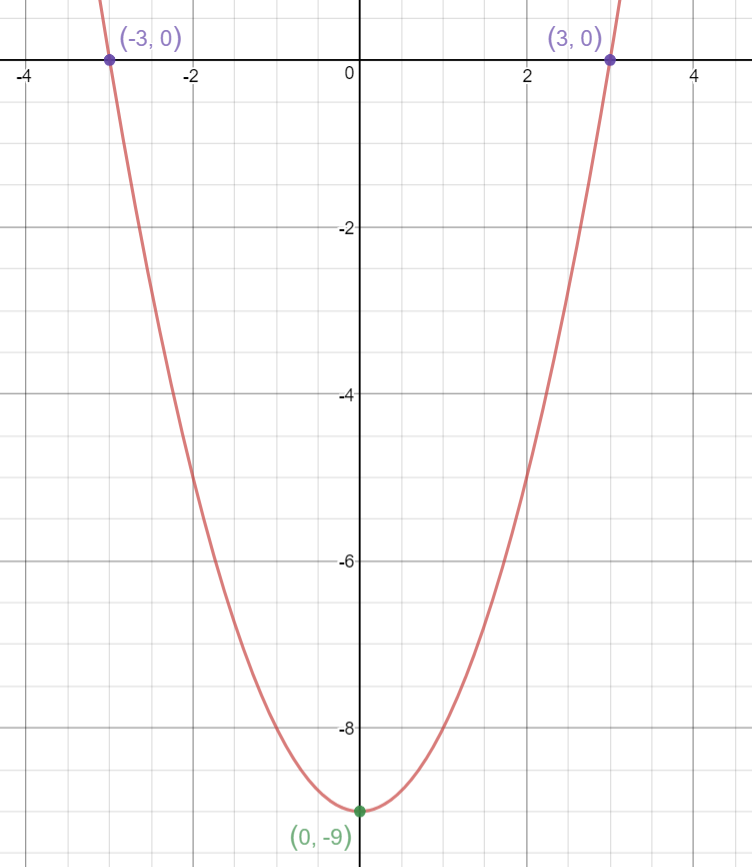



How Do You Graph Y X 2 9 Socratic
The most general form of a quadratic function is, f (x) = ax2 bx c f ( x) = a x 2 b x c The graphs of quadratic functions are called parabolas Here are some examples of parabolas All parabolas are vaguely "U" shaped and they will have a highest or lowest point that is called the vertexMath Algebra Parabola Graph y = x^2 and x = y^2 on a 2D planePolynomials quadratics conicsections Share edited 1 min ago Gary




6 2 Graphing Parabolas Function Language And Graphing With A Table Ppt Video Online Download




Graph Of Y X 2 The Equation For A Parabola Download Scientific Diagram
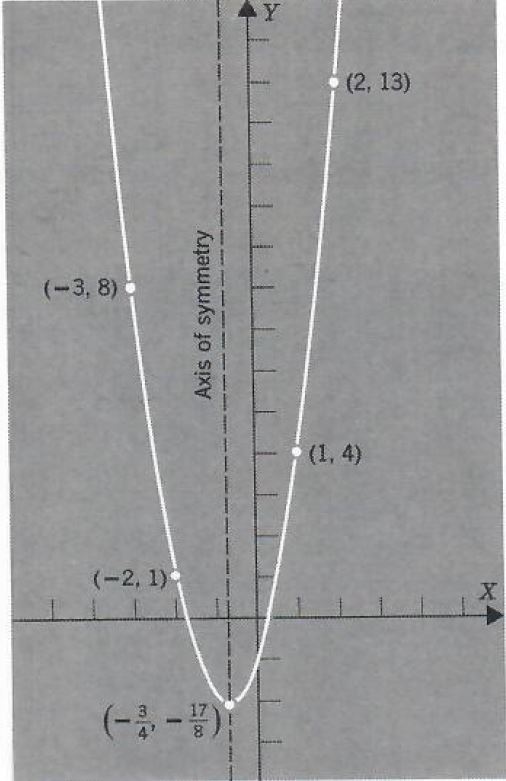
The general equation of a parabola is y = a(xh) 2 k or x = a(yk) 2 h, where (h,k) denotes the vertex The standard equation of a regular parabola is y 2 = 4ax Some of the important terms below are helpful to understand the features of a parabola Focus The point (a, 0) is the focus of the parabolaGraph the parabola, y =x^21 by finding the turning point and using a table to find values for x and yShifting the Graph of a Parabola The one main thing required to learn how to shift the parabola is to actually read the equation Let's take an example In the equation y=x² It has a vertex at the points (0,0) and tends to open upwards The points on it are (1, 1), (1, 1), (2, 4), and (2, 4) Shifting a Parabola Upwards Let's make an



What Is The Area Bounded By The Curve Y 2 2x 1 And X Y 1 0 Quora




Graph Of Y X 2 The Equation For A Parabola Download Scientific Diagram
So the parabola has its vertex to the left on the y axis at (0,2) and its axis is a horizontal line parallel to the x axis with formula y = 2 It is symmetric about this axis The means that for every point (x,y) that lies on the parabola, so does the point (x,(4 − y)) The lower 'arm' of the parabola will intersect the x axis when y = 0Take several values for and find , make a table xy 00 13/2 Once you know the axis of symmetry, you can plug that value in for x to get the y coordinate These two coordinates will give you the vertex of the parabola In this case, you would plug 0 in to 2x 2 1 to get the y coordinate y = 2 x 0 2 1 = 0 1 = 1 The vertex is (0,1), and the parabola crosses the yaxis at 1



Solution Please Help Me With Those Problems Thanks 1 Graph X2 2xy Y2 1 2 If The Parabola De Fined By Y Ax 2 6 Is Tangent To The Line



Quadratics Graphing Parabolas Sparknotes
X 2 = 4py The graph of the parabola would be the reflection, across the x axis of the parabola in the picture above A way to describe this is if p > 0, the parabola "opens up" and if p 0 the parabola "opens down"Set y y equal to the new right side y = − x 2 y = x 2 y = − x 2 y = x 2 Use the vertex form, y = a ( x − h) 2 k y = a ( x h) 2 k, to determine the values of a a, h h, and k k a = − 1 a = 1 h = 0 h = 0 k = 0 k = 0 Since the value of a a is negative, the parabola opens down Opens DownGraphing Parabola A parabola is one of the conic sections In order to graph a parabola, we must know first the standard equation The standard equation of a parabola is {eq}(xh)^2=4p(yk) {/eq}



Find The Vertex Focus And Directrix Of The Chegg Com



Graph The Parabola Y X 2 6x Mathskey Com
Consider the parabola y = x 2 Since all parabolas are similar, this simple case represents all others Construction and definitions The point E is an arbitrary point on the parabola The focus is F, the vertex is A (the origin), and the line FA is the axis of symmetry The line EC is parallel to the axis of symmetry and intersects the x axisAxis\(y3)^2=8(x5) directrix\(x3)^2=(y1) parabolaequationcalculator en Related Symbolab blog posts Practice Makes Perfect Learning math takes practice, lots of practice Just likeNormals to a Parabola The graph shows the normal lines from the point (2,0) to the graph of the parabola x=y^{2} How many normal lines are there from the poi 🎉 Announcing Numerade's $26M Series A, led by IDG Capital!



Quadratic Function Parabola




Parabola Wikipedia
Change a, Change the Graph Another form of the quadratic function is y = ax 2 c, where a≠ 0 In the parent function, y = x2, a = 1 (because the coefficient of x is 1) When the a is no longer 1, the parabola will open wider, open more narrow, or flip 180 degrees Examples of Quadratic Functions where a ≠ 11 day ago I had this question and saw the other thread, and the proof of why all quadratics were parabolas started with the axiom that y = x 2 is a parabola well I don't really understand why y = x 2 is a parabola I get that if you plot it you get a parabola, but why is that the case?In the graph of y = x2, the point (0, 0) is called the vertex The vertex is the minimum point in a parabola that opens upward In a parabola that opens downward, the vertex is the maximum point We can graph a parabola with a different vertex



Solution How To Graph X Y 2 6y 8 This Is Parabola



Quadratics Graphing Parabolas Sparknotes
A parabola has the equation $$x (y 2)^2 = 0$$ I can't find the $y$ without getting the equation into some weird recursionParabola The standard form equation of a general quadratic (polynomial functions of degree 2) function is f(x) = ax 2 bx c where a ≠ 0 If b = 0, the quadratic function has the form f(x) = ax 2 c Since f(x) = a(x) 2 c = ax 2 c = f(x), Such quadratic functions are even functions, which means that the yaxis is a line of symmetry of the graph of fThe procedure to use the parabola graph calculator is as follows Step 1 Enter the parabolic or quadratic equation in the input field Step 2 Now click the button "Submit" to get the percent Step 3 Finally, the graph will be displayed in the new window



How To Draw Y 2 X 2 Interactive Mathematics
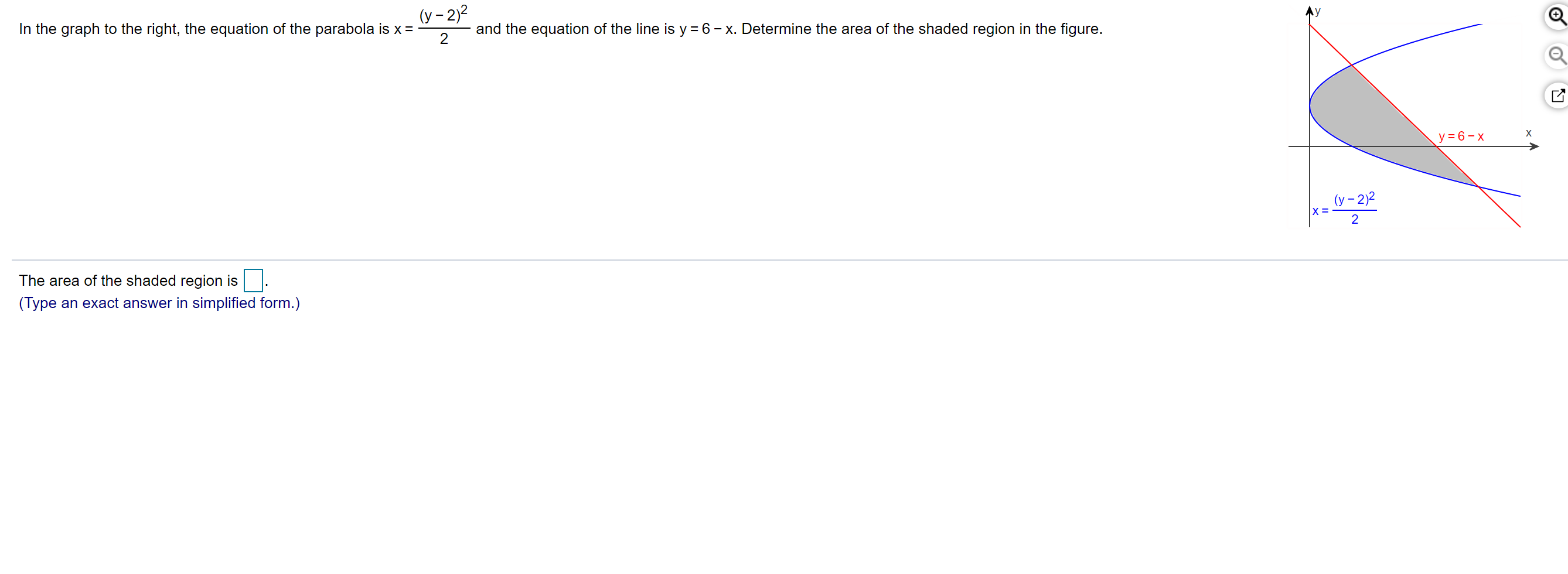



In The Graph To The Right The Equation Of The Chegg Com
Let's try sketching the graph of the quadratic function {eq}y=f(x)=x^2A parabola has equation y = x^2 2x 3 The graph of the parabola is shifted one unit to the right What is the new equation?Examples with Detailed Solutions Example 1 Graph of parabola given x and y intercepts Find the equation of the parabola whose graph is shown below Solution to Example 1 The graph has two x intercepts at \( x = 1 \) and \( x = 2 \) Hence the equation of the parabola may be written as \( y = a(x 1)(x 2) \) We now need to find the coefficient \( a \) using the y intercept at \( (0,2
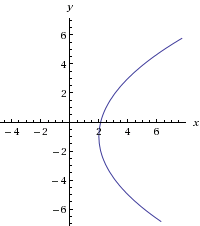



How To Graph A Parabola X 2 1 8 Y 1 2 Socratic




Graphing Questions
Click here to see ALL problems on Graphs Question 6355 Graph the parabola y= 3/2 x^2 Answer by MathLover1 () ( Show Source ) You can put this solution on YOUR website!Join the MathsGee Answers & Explanations community and get study support for success MathsGee Answers & Explanations provides answers to subjectspecific educational questions for improved outcomesFirst, let's look at the graph of a basic parabola y=x2, where a=1, b=0, and c=0 Notice the graph opens up, the vertex is at x=0, and the yintercept is at y=0 Let's vary the value of ato determine how the graph changes Let's graph y=x2 (blue), y=¼x2(green), y=½x2 (purple), y=2x2(red), and y=4x2 (black) on the same axes



1



Fcwcfm1ishpgqm
As you indicated the parabola x = y 2 is "on its side" x = y 2 You can determine the shape of x = 4 y 2 by substituting some numbers as you suggest Sometimes you can see what happens without using specific points Suppose the curves are x = y 2 and x = 4 y 2 and and you want to find points on the two curves with the same yvalue ThenGraph horizontal parabolas (x = a y 2 b y c or x = a (y − k) 2 h) (x = a y 2 b y c or x = a (y − k) 2 h) using properties Step 1 Determine whether the parabola opens to the left or to the right Step 2 Find the axis of symmetry Step 3 Find the vertex Step 4 Find the xintercept Find the point symmetric to the xinterceptExploring Parabolas by Kristina Dunbar, UGA Explorations of the graph y = ax 2 bx c In this exercise, we will be exploring parabolic graphs of the form y = ax 2 bx c, where a, b, and c are rational numbers In particular, we will examine what happens to the graph as we fix 2 of the values for a, b, or c, and vary the third We have split it up into three parts



Exploration Of Parabolas




Understand How The Graph Of A Parabola Is Related To Its Quadratic Function College Algebra
Graphs of quadratic functions all have the same shape which we call "parabola" All parabolas have shared characteristics For example, they are all symmetric about a line that passes through their vertex This video covers this and other basic facts about parabolasThe graph of the quadratic function is a Ushaped curve is called a parabola The graph of the equation y = x 2, shown below, is a parabola (Note that this is a quadratic function in standard form with a = 1 and b = c = 0) In the graph, the highest or lowest point of a parabola is the vertex The vertex of the graph of y = x 2 is (0, 0)The General Equation for a Parabola is Y = AX² BX C where A, B & C are Real numbers B & C can be zero, and A can be any value except zero For example Y = 2X² 3X 1 is a typical parabola which is "vertex down" as shown in Graph 1 below
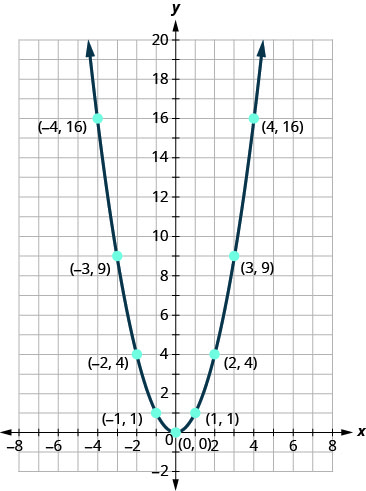



9 8 Graph Quadratic Functions Using Transformations Mathematics Libretexts
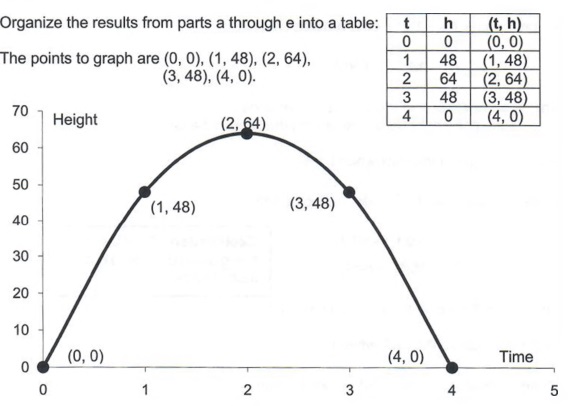



Graph Graph Equations And Equation Systems With Step By Step Math Problem Solver
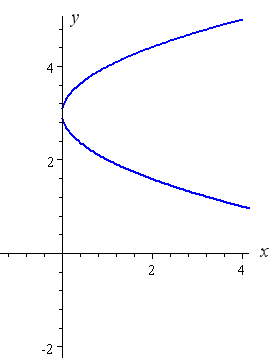



How To Draw Y 2 X 2 Interactive Mathematics




Graphing Quadratic Functions A Quadratic Function Is An Equation Of The Form Y Ax 2 Bx C Ppt Download




Sketch The Region Enclosed By The Curves Y 2 2x 6 And Y X 1 And Find The Area Youtube




Quadratic Function Wikipedia




Graphing Parabolas
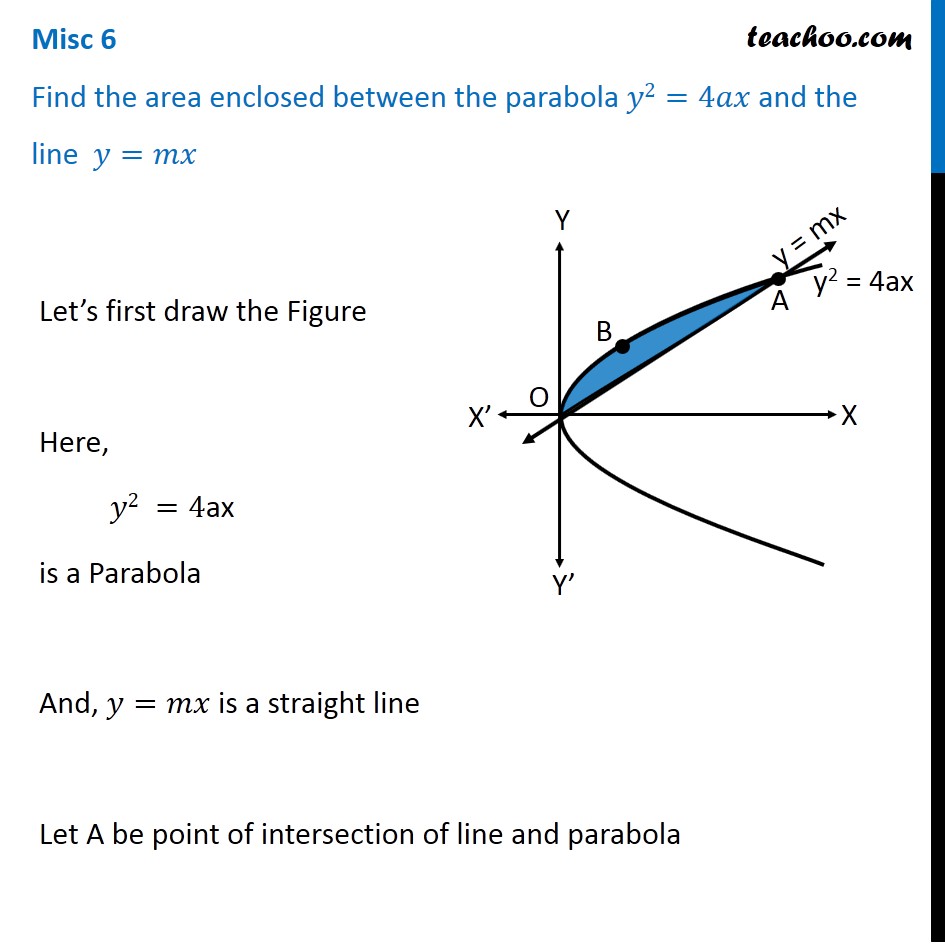



Misc 6 Find Area Enclosed Between Parabola Y2 4ax And Y Mx




Equation Of Parabola In X Y Plane Mathematics Stack Exchange



Graph Graph Equations And Equation Systems With Step By Step Math Problem Solver



How To Draw A Sketch Of The Graph Of The Parabola Y X 2 8x 10 Quora



What Is The Graph Of Xy 2 Quora



Find The Area Of The Region Included Between The Parabola Y2 X And The Line X Y 2 Quora




View Question The Graph Of Y 2x 4 X 4 Is A Parabola In The Xy Plane In Which Of The Following Equivalent Expressions Do The X And Y Coordinates Of



Comparing The Graphs Of A Quadratic And A Related Equation




How To Draw Y 2 X 2 Interactive Mathematics



The Parabola Below Is A Graph Of The Equation Y X 1 2 3 Mathskey Com
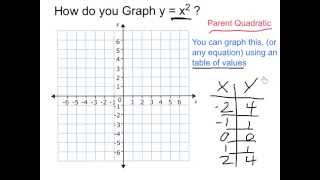



Graph Y X 2 Youtube
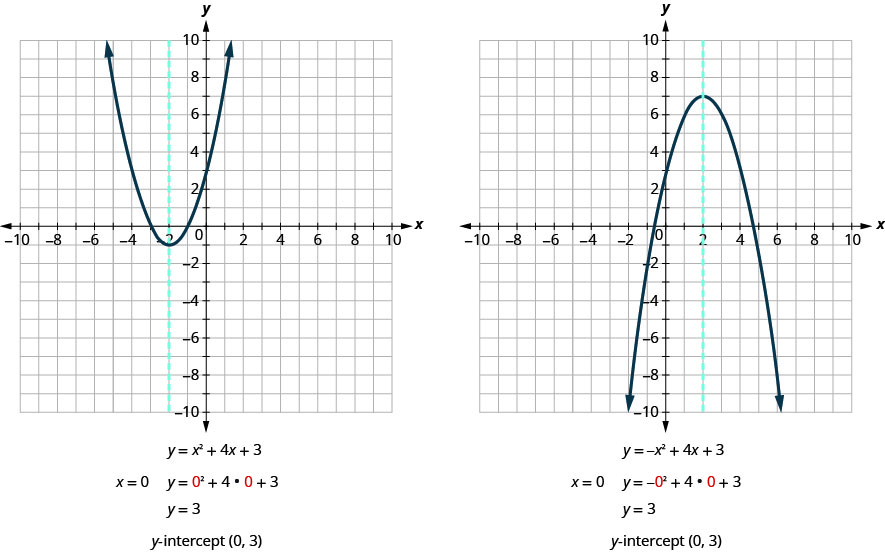



10 5 Graphing Quadratic Equations Mathematics Libretexts
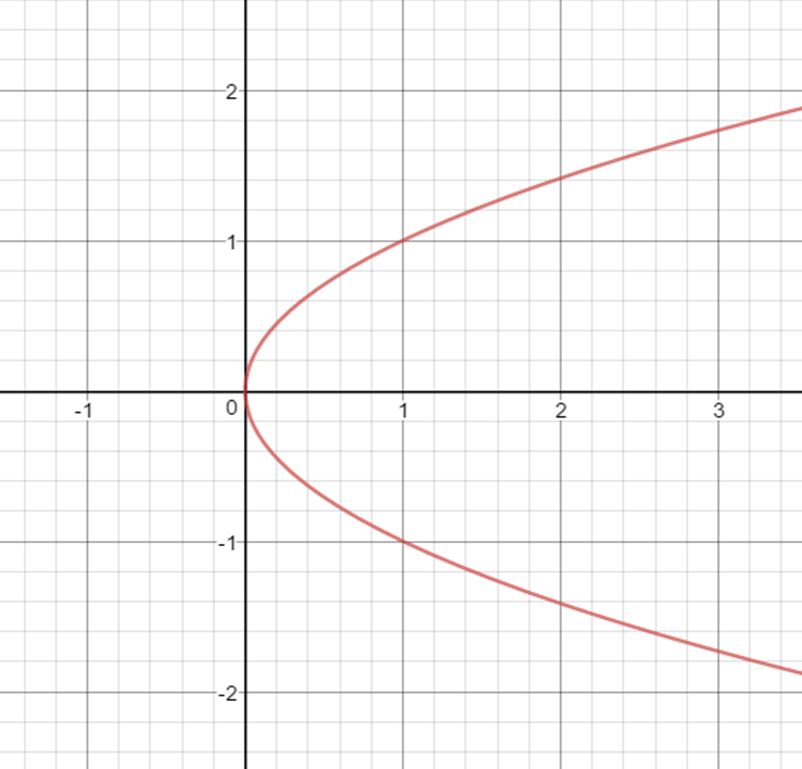



Example Of A Horizontal Parabola X Ay Expii




Surfaces Part 2
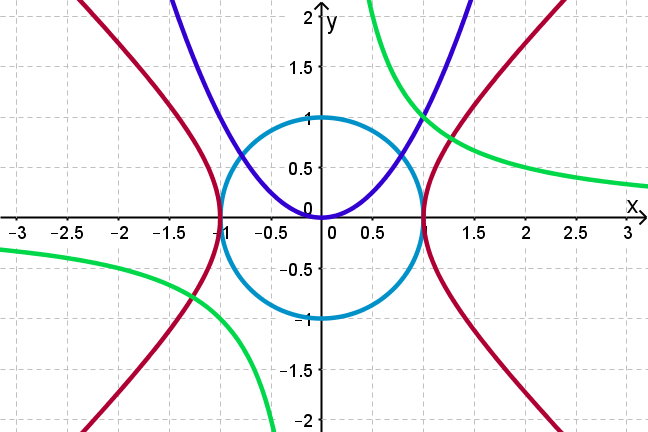



Conic Sections As Second Degree Curves



How Do You Sketch The Graph Of Y X 2 8 And Describe The Transformation Socratic




Graphing Parabolas




Quadratic Function




How To Graph A Parabola 13 Steps With Pictures Wikihow



Graphing Quadratic Functions




Graph Y X 2 3 Youtube




Graphing Quadratic Functions Lesson Article Khan Academy



Quadratics Graphing Parabolas Sparknotes



Conic Sections Parabola Equation Of A Translated Parabola The Standard Form




Graphing Quadratic Functions Lesson Article Khan Academy



X Y 2 And X 4 Y 2 Math Central
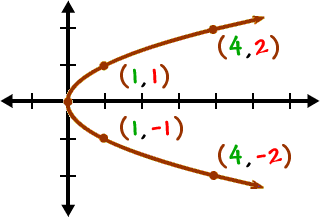



Sideways Parabolas 1
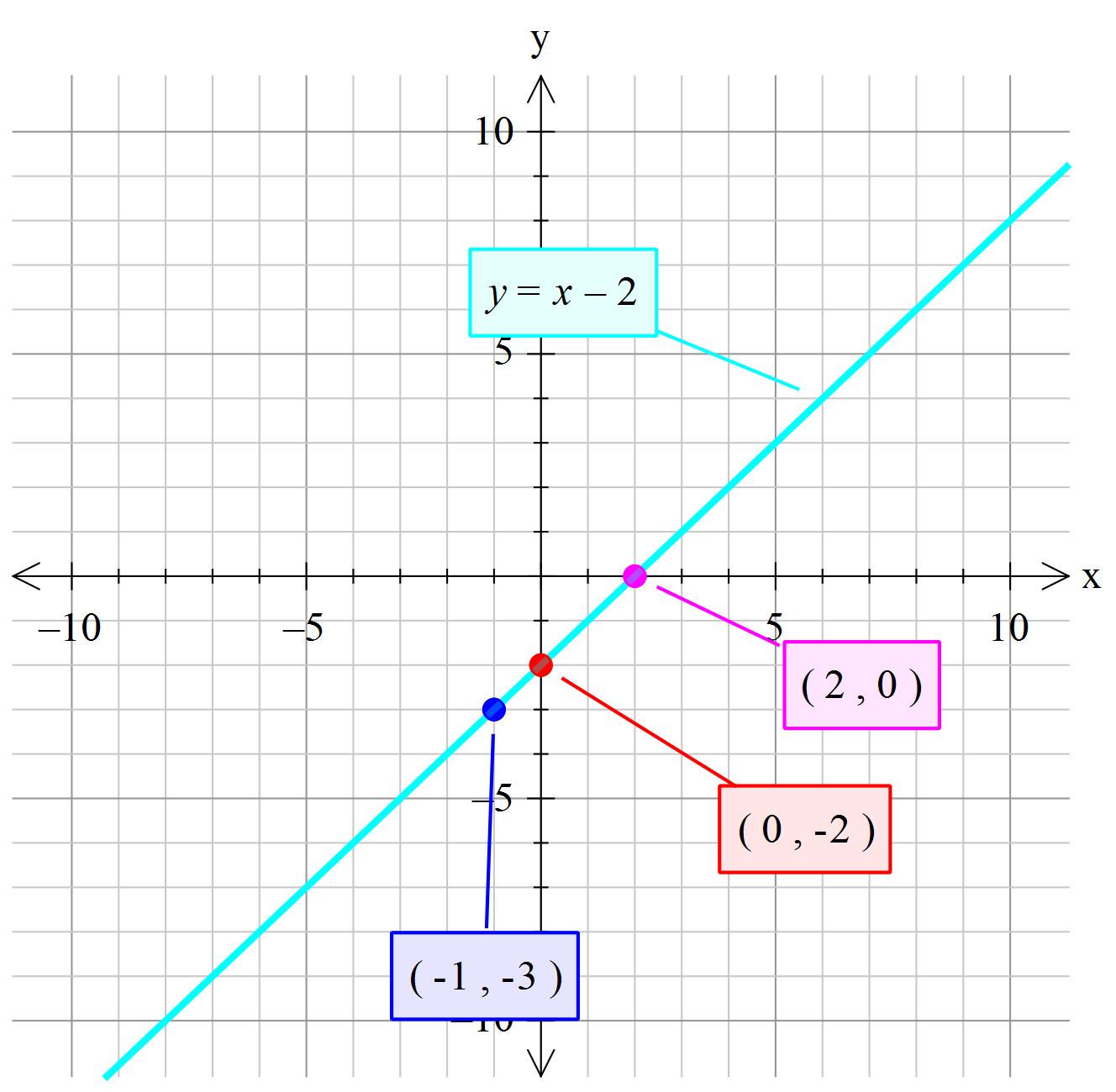



How Do You Graph The Line X Y 2 Socratic




Plot A Parabola Mapleprimes
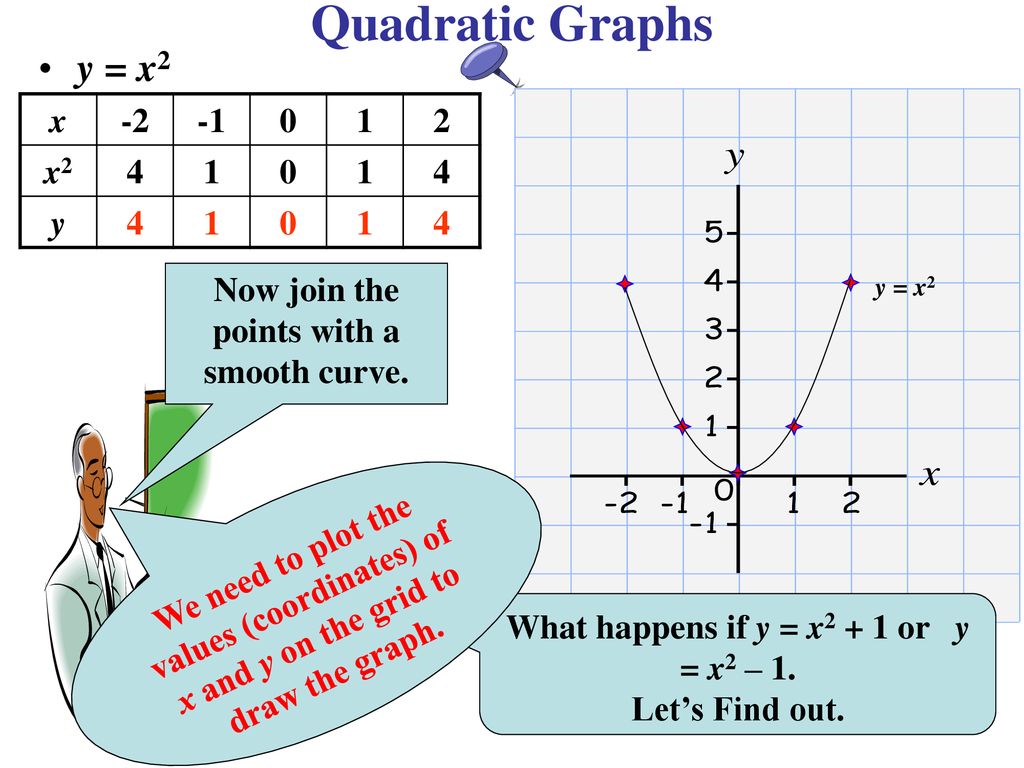



Quadratic Graphs Parabolas Ppt Download



Content Transformations Of The Parabola



1




Evaluating Area Between Two Curves X 4 Y 2 And X Y 2 For Dx And Dy Mathematics Stack Exchange



Intersection Of Line And Parabolla Zona Land Education
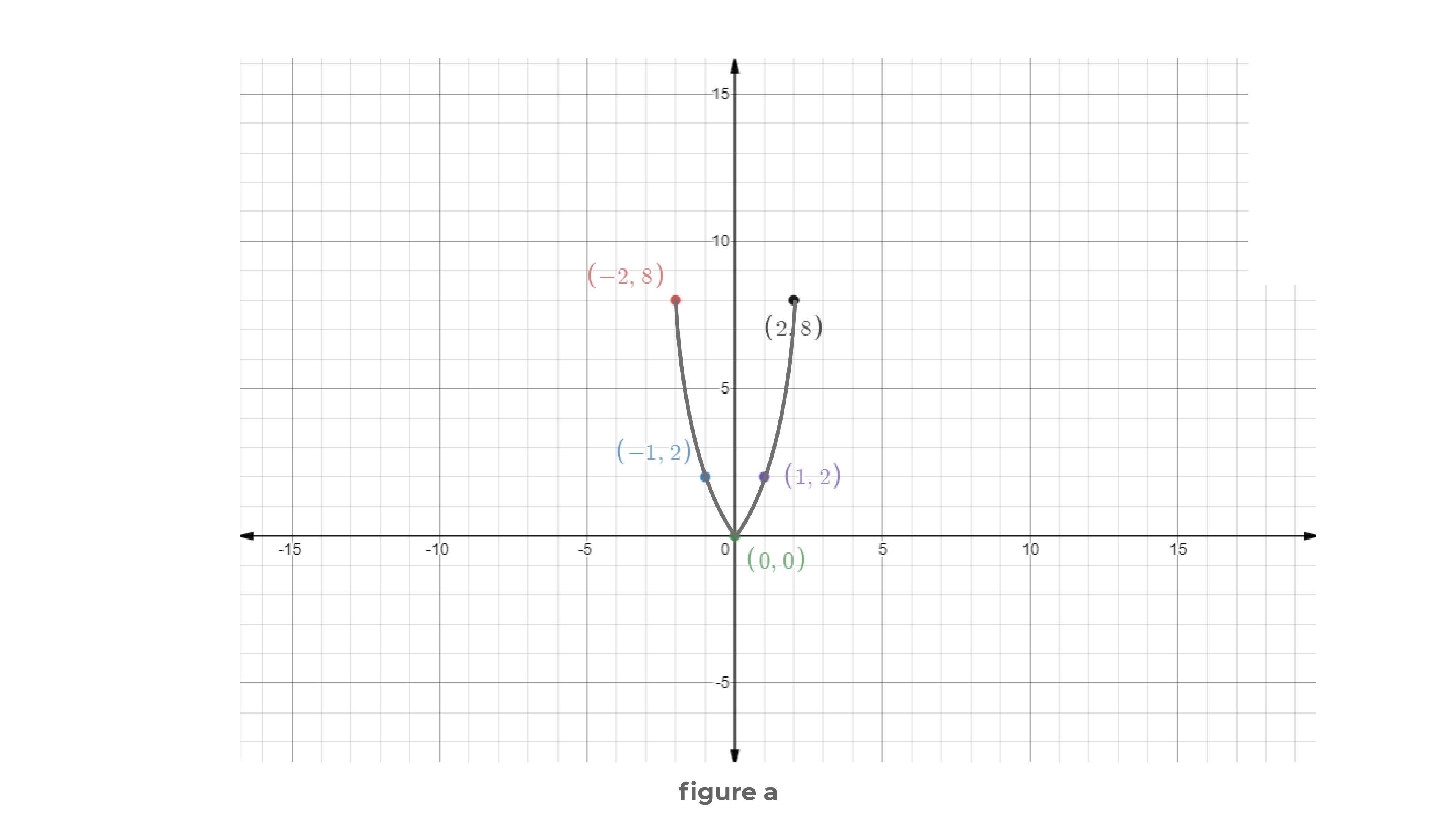



Study The Table X Y 2 8 1 2 0 0 1 2 2 8 Which Best Describes The Function Represented By The Data In The Table




Graphing Parabolas



X Y 2 And X 4 Y 2 Math Central



Content Transformations Of The Parabola




How To Graph A Parabola 13 Steps With Pictures Wikihow
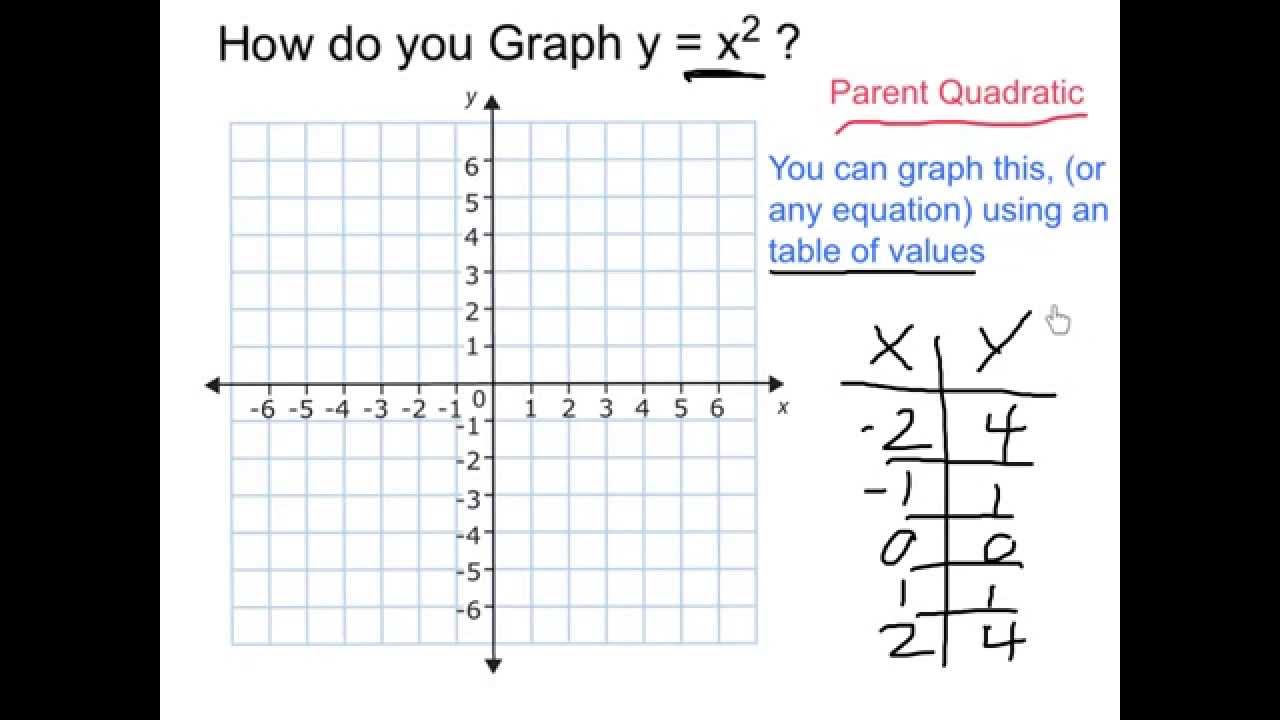



Graph Y X 2 Youtube
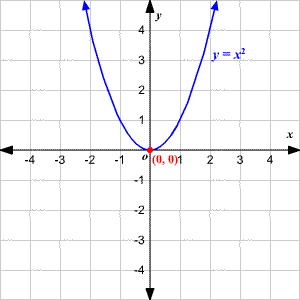



Parabolas



Content Transformations Of The Parabola




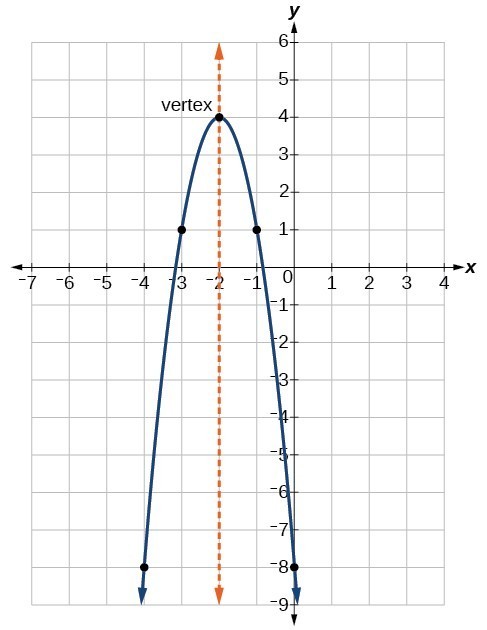
Characteristics Of Parabolas College Algebra




Graphing Parabolas
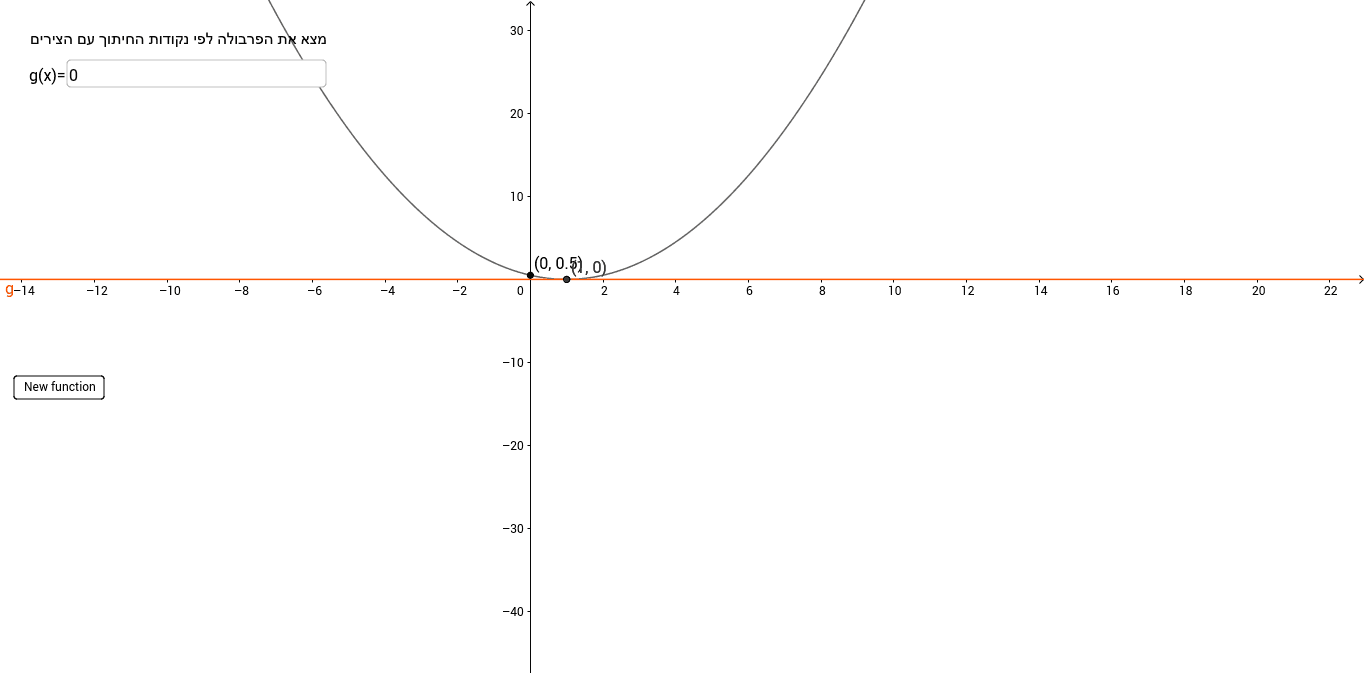



Parabola Match Graph To Function X Y Intersection Points Geogebra



Quadratic Functions




How To Graph A Parabola In A Cartesian Coordinate System Owlcation
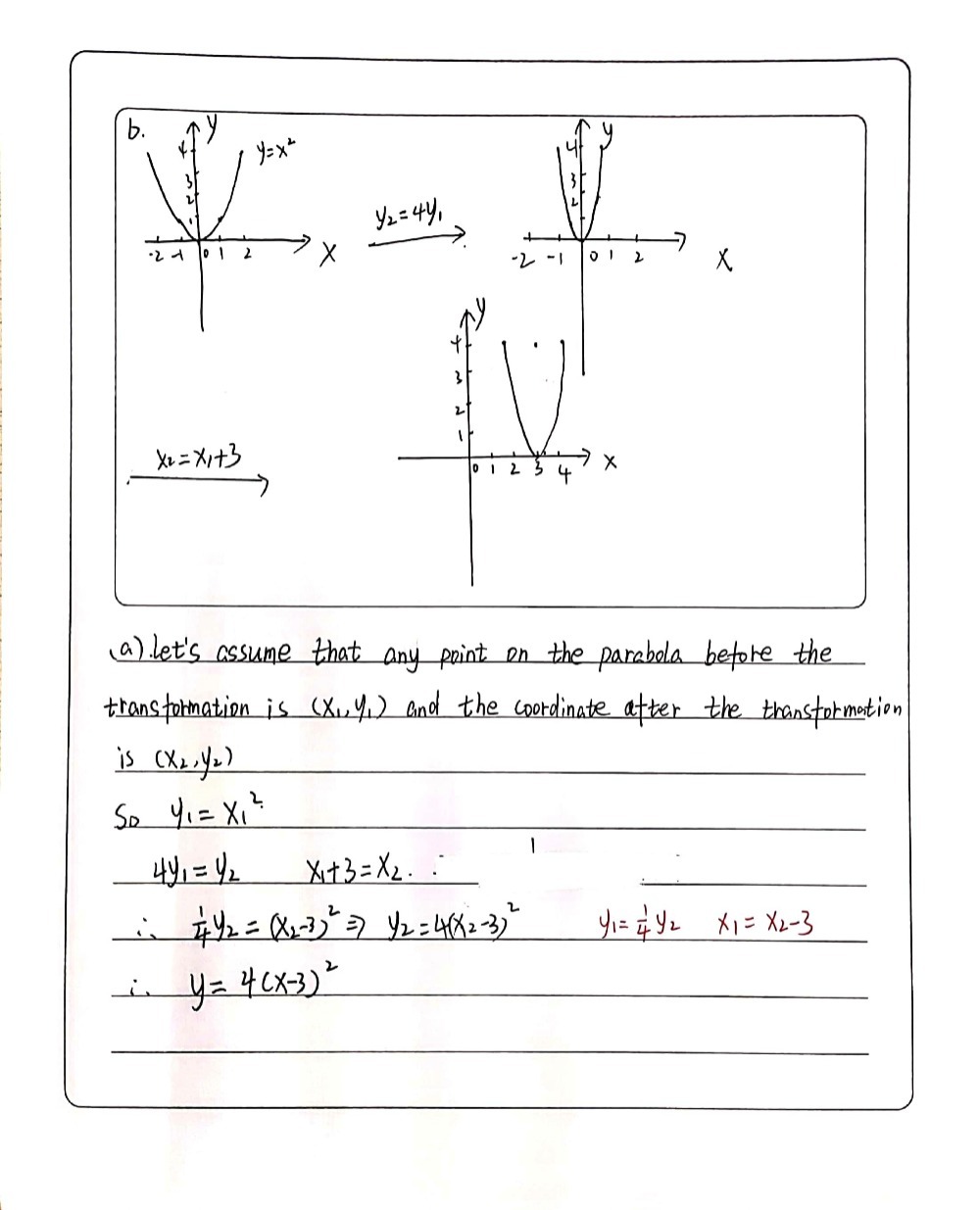



The Graph Of Y X2 Is Stretched Vertically By A F Gauthmath
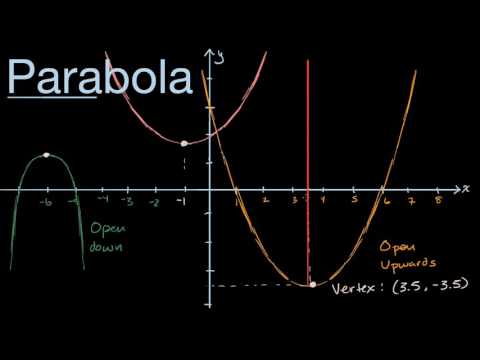



Parabolas Intro Video Intro To Parabolas Khan Academy




Solution For The Parabola Y X 2 36 Graph Of A Parabola Opening Down At The Vertex 0 36 Crossing The X Axis At 6 0 And 6 0




What Does X Y 2 Look Like On A Graph Study Com




How To Draw Y 2 X 2 Interactive Mathematics




Parabola The Set Of All Points That Are Equidistant From A Given Point Focus And A Given Line Directrix Ppt Download
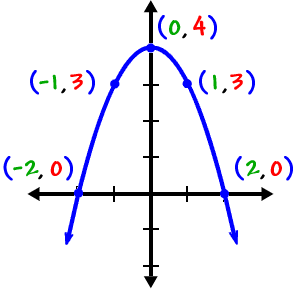



Graphing Quadratics Parabolas Cool Math Algebra Help Lessons Graphing Parabolas Overview




Quadratic Function



Vertex And Intercepts




How To Graph A Parabola 13 Steps With Pictures Wikihow
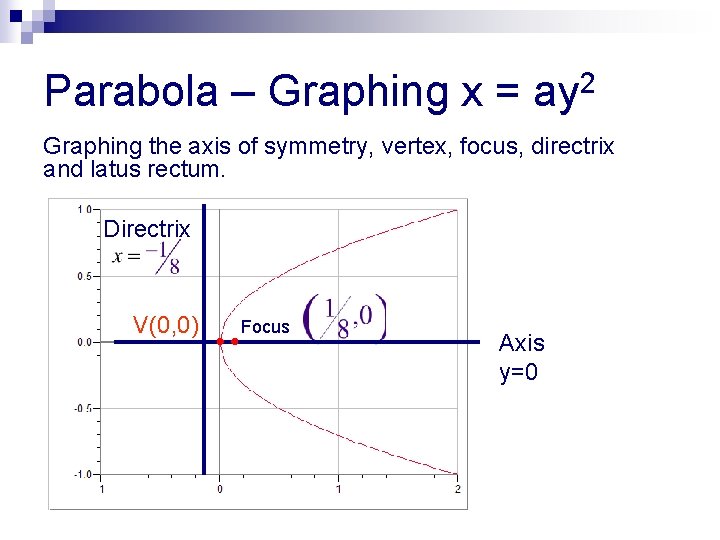



Conic Sections 11 1 Parabola Conic Sections Parabola



Quadratics Graphing Parabolas Sparknotes



Graphing Quadratic Functions




Graphing A Parabola Of The Form Y2 Ax Practice Study Com




How To Draw Y 2 X 2 Interactive Mathematics
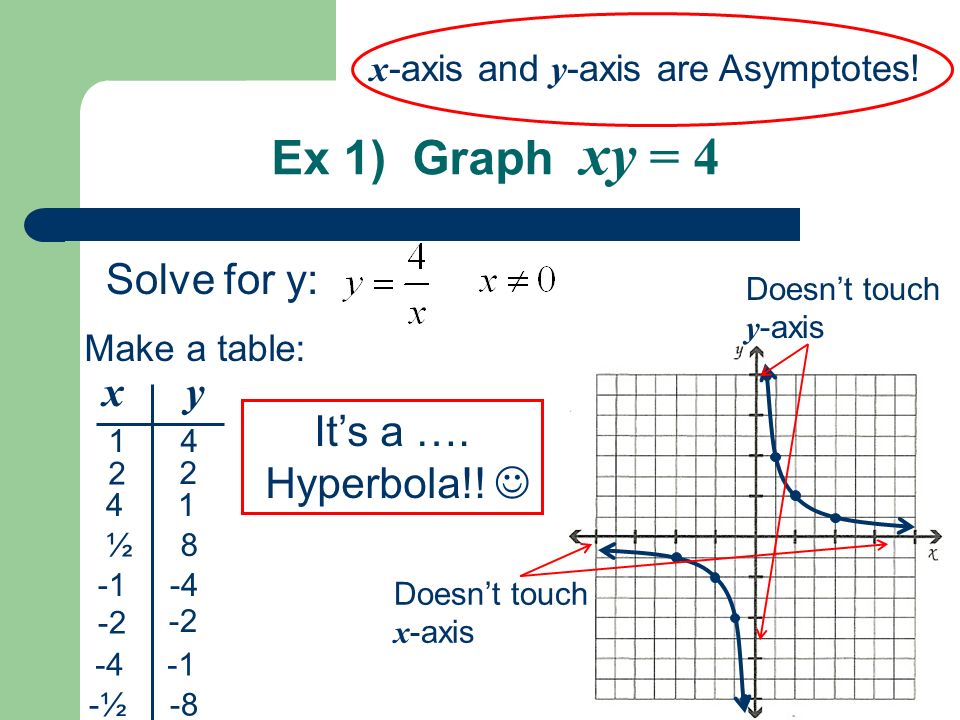



10 1 Identifying The Conics Ex 1 Graph Xy 4 Solve For Y Make A Table Xy Doesn T Touch Y Axis Doesn T Touch X Axis Ppt Download



Parabolas




Graphing Quadratic Functions Lesson Article Khan Academy



Content Parametric Equations Of A Parabola
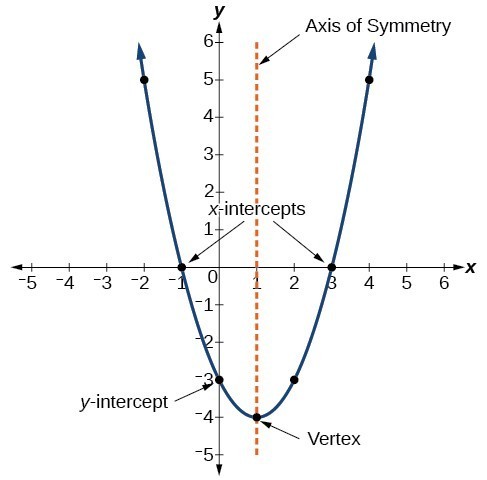



Characteristics Of Parabolas College Algebra



Graphs Of Equations



Fcwcfm1ishpgqm



0 件のコメント:
コメントを投稿